圆周率Pi(
)为圆周长与其直径的比值,通常近似为3.14159。在美剧《疑犯追踪》第2季11集就提到了这个最著名的数学常数,该集里主角芬奇先生是一名代课老师,他在黑板上写了3.1415926535。然后他问学生们:“这意味着什么?”
我在脑海中立马冒出了这个问题的答案,心想:“如果我有一个直径为1的自行车轮胎,那么这个自行车轮胎旋转一周行驶的距离就是
。”然而,在电视剧中,没有学生如此回答。
见如此场景,芬奇先生自己给出了答案,他说:“
是圆的周长与直径之比,3.141592635仅仅只是这个比值的前几位,它本身是一个无限不循环小数,小数点后有无限个数位,并且永不重复;你的出生日期,储物柜的密码,你的社会保险号码等等都在这个数字串的某一处。如果你把这些数转换成字母,这些字母可以组成任何一个存在的单词,这些字母可以是婴儿发出的第一个音节,可以是你心上人的名字,可以是你这一生中的所有故事的描写,可以是我们说过的或者做过的每一件事情。世界上所有无限的可能性都存在于这个简单的圆里。现在你将如何处理这些信息;它有什么好处?这取决于你…”

▲《疑犯追踪》该集的剧照
这样极具戏剧的一幕,虽并不准确(马上就会谈到),也让我称赞不已。因为现实中有很多人都努力要成为(或者有)像芬奇所饰演优秀且有趣的教师。这样的教师不仅能引导学生们讨论课本以外的知识,而且还能让其全神贯注在课堂之中。
不过话说过来,芬奇先生所说并非100%正确的,因为数学家还没有证明
为正规数。换句话说,数学家们尚未知
是否包含从0到9的所有有限的数字排列。
数学上,粗略来说,正规数指,数字显示出随机分布,且每个数字出现机会均等的实数。
没有人知道如果数学家继续研究下去会发现什么。比如,当我们观察
的前10亿位时,我们看到数字7出现了将近1亿次。这使得
成为一个很好的随机数生成器。但是,在某些点之后,
可能不包含7,可能是一个只有两个或三个数字的不循环重复的数字,例如会出现010203112233000111222333这样诡异的序列。
这里要提到一个著名的示例,在
的前761位之后,有一个著名的数学巧合,即连续出现6个9,这被称之为费曼点(“Feynmanpoint”).

但人们相信
的小数位会以一种随机的顺序永远持续下去,这就变得有趣了,它无限不循环,但同时它又是一个确定的数值。这并不矛盾,因为
是圆的周长和直径的比值,所以它是一个有确定值的数学常数。当然,通常的计算中,我们只需要
的近似值就够了。
在1768年,瑞士数学家约翰·海因里希·朗伯证明了
的值是无理数,所以它不能写成分数的那样形式。在那之前22/7就经常被用来当作
的近似值,虽然它实际上并不等于
。我们都知道无理数不能写成两个整数的比值(即分数,像a/b的形式),因为无理数是无限的,且不循环的小数。
再后来1882年,德国数学家费迪南德·冯·林德曼证明了
是一个超越数,即不是任意整系数代数多项式的根。
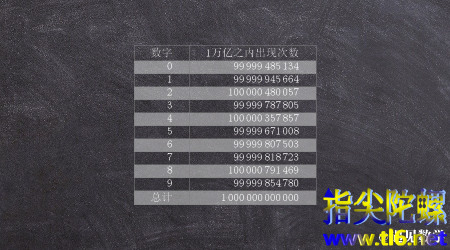
数学家金田康正(YasumasaKanada)发现圆周率的前万亿个数字在统计学上是随机的。如果你查看下表,你会发现每个数字发生的事件是独立的,发生的概率约是十分之一。
▲圆周率中连续的六个9
许多年之后的2019年,谷歌女工程师EmmaHarukoIwao利用云计算资源,花了121天计算出
的34.1万亿位。你可以在你脑海中想象这样的画面:如果要用普通字体打印
小数点后的10亿位,它的长度将从美国纽约延伸到堪萨斯州!
然而,34.1万亿位这么巨大的数字仍然不足以在数学上证明
是正规数成立。超级计算机仍在尝试挑战计算更精确的
。你查看下面的图表就会看到自公元前250年以来,历史时间轴图上探索圆周率的已知位数。
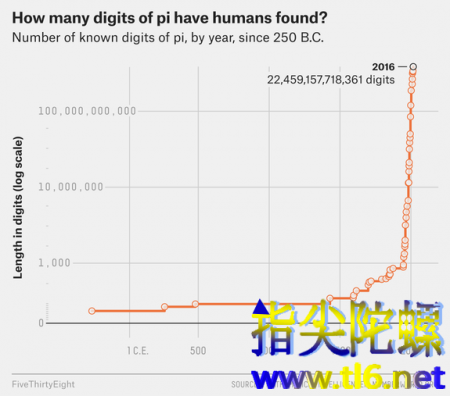
▲当数学家发现新的算法、电脑变得普及时,
的已知小数位呈指数增加。注意垂直坐标使用了对数坐标
再回到文章提到这部美剧中芬奇先生,我们明白他所说的也非错误。你可以很轻松地在
中找到自己的生日。如果你登陆这个网址mypiday.com输入你的生日,上面就会显示它在
中的位置。
如果
是一个正规数,那可以说我们的整个命运都是用
编码,将来发生的一切画面(图片是二进制文件)都将在
里揭示,甚至这篇文章也在
里某个位置默默存在。从这一点来说芬奇先生其实是正确的。接下来我们用一种有趣并且充满艺术性的方式来展示
的随机性。
尽管在科学家们眼中那些单调乏味的散点图并不枯燥,但是数据艺术家们利用色彩对其进行数据可视化之后,它们就变得容易被大众欣赏接受。MartinKrzywinski就是这样一个艺术家,他探索
的艺术之美,他给
中的每个数字赋予一种不同的颜色。比如,他让橙色表示3,红色表示1,黄色表示4等等。然后他做了一张美丽的海报(第2副)。这样如果你仔细看,就看不到任何特别模式的图案。
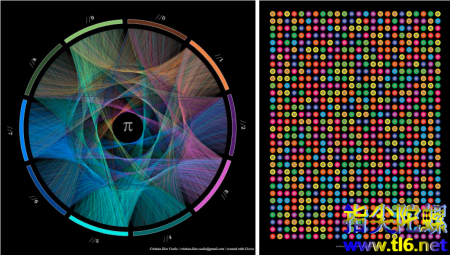
▲MartinKrzywinski所设计的可视化作品
除了有这么多引人入胜的事实之外,圆周率也是迄今为止数学史上研究最多的数字。几个世纪以来,数学家一直在努力计算更精确的圆周率值。人类到底应该停下来研究
的其他性质,还是应该继续探究一个
的更精确的值?还是假定
=3.14就足够了?要知道用40位的
来计算银河系的周长,而误差还不到一个质子的直径。
有成百上千的数学家多年来一直在试图找出圆周率的更多数字。这就像试图到达月球,然后下一个目标就是到达火星,以此类推……但为什么?为什么数学家要费心计算更多的位数呢?为什么34.1万亿位的
还不够?是因为圆周率蕴藏在每一个圆之中吗?
▲每一次旋转都是有
的身影
我们给出看着晦涩难懂但其实是合乎逻辑的理由,因为
是产生随机数的来源。尽管现实的原因可能是各国可以借此向他国炫耀自己的科技水平,因为计算万亿位数的
需要一台非常强大的计算机。比如在《星际迷航:WolfintheFold》剧集中,斯波克就施计让邪恶的计算机“给出
的最后一个数字”,以此来永远阻塞它下一步企图。
另一方面,我们人类总是去尝试攀登更高的山,潜入更幽深海沟……或者尝试着去记住
小数点后面更多的数字,比如吕超,他准确无误地背住了
小数点后的前67890位。人们一直都在挑战做这些尝试是因为想要更了解所生活的这个世界。
在1962年9月12号,约翰肯尼迪(JohnF.Kennedy)发表了一篇关于太空计划的演讲。
“为什么选择登月作为我们的目标?那他们也许会问为什么我们要登上最高的山峰?为什么,要在35年前,飞越大西洋?为什么赖斯大学要与德克萨斯大学竞赛?我们决定登月。我们决定登月。我们决定在这十年间登上月球并实现更多梦想,并非它们轻而易举,而正是因为它们困难重重。因为这个目标将促进我们实现最佳的组织并测试我们顶尖的技术和力量,因为这个挑战我们乐于接受,因为这个挑战我们不愿推迟,因为这个挑战我们志在必得,其他的挑战也是如此。”
回溯过去,
贯穿着整个人类历史。这就是为什么我们可以说,只要有人类存在,总会有人想知道它的下一位是什么。而且我确定,在这个世界的某个地方里一定有数学家或者科学家正在利用
去探索我们宇宙中的奥秘,因为
仍然是自然界的神秘常数。
探究
之路
数学有着久远的历史,与人类文明一样古老。
被人类研究了近4000年。早在公元前1700年,当世界上最后一头猛犸象倒下之际,人们就已估算至前两位(“3”和“1”)。
来自古希腊的阿基米德便是最早计算圆周率的智者之一。当时他可能是设计制造车轮的过程中接触到这个神秘的常数。但是他究竟是怎么估计出
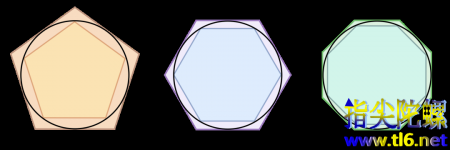
的约值呢?他先是把所有的多边形都看作是圆,据他所说,如果持续增加多边形的边数,就会得到一个接近完美的圆。换句话说,五边形比正方形更圆,而六边形比五边形更圆,等等……就这样,传奇数学家阿基米德在两千多年前就把圆定义为一个边数极大的正多边形。
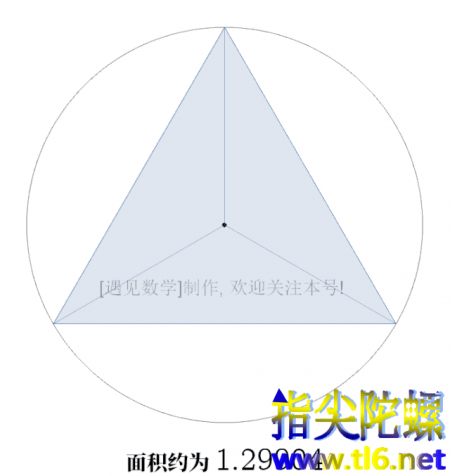
他所采用这种通过正多边形的几何算法是有用的,因为当时人们很难精确地测量曲面。首先,他做了已知周长的正方形的外接圆,然后在这个外接圆的外面画第二个正方形,满足外接圆是第二个正方形的内切圆并求出该正方形的周长。这样他就得到了圆的周长应该是介于两个正方形的周长之间。然而利用这种方法计算出来的两个正方形的周长差值比较大。因此他又把正方形换成五边形来重新计算圆周的上下界,他得到了一个较小的圆周的界限。之后,他不断地增加圆内切和外接多边形的边数。
▲阿基米德使用穷竭法通过计算外接多边形和内接多边形的周长来估计
边数每增加一,对
的估值就更精确一些。他一直计算到96条边的正多边形,[英文:Enneacontahexagon]此时圆的周长位于
(3.1408and3.1429之间)。因此,他计算
到小数点后的精确两位。阿基米德的手动计算方法当然还可以再改进,这样也让他穷尽一生都没有达成。
而我国南北朝刘宋时代杰出的数学家、天文学家祖冲之利用割圆术计算正24576边形的边长,得到π≈355/113,其小数点后的前六位数都是正确值。这样的结果在之后的八百年内,都是准确度最高的
估计值。
数学家们需要去找到更有效的公式和更新的数学方法。微积分的发明使得
的计算有了一次大的飞跃。之后,数学家开始用无穷级数的方式来计算
。无穷级数是有序的无穷个数字和的表达式,而且收敛的无穷级数会得到一个特定的值。
当今世界人类有很多方法去计算
,最早的格雷果里-莱布尼茨公式如下图所示。这样利用无穷级数去表示反正切函数arctanx,把无穷多个小数加到一起计算出了
。
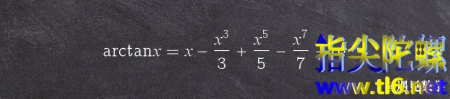
当x=1代入方程即能求得
/4的值。人们所展开的项越多,结果越趋近于
。不过该级数收敛速度实在太慢,为了精确得到
小数点后10位,我们要把大约50亿项加起来才好。
探究
的道路上再往后发展,另一位伟大的数学家欧拉(LeonhardEuler)登场。在他28岁(1735年)的时候为解决当时难倒欧洲所有数学家的一个难题,为圆周率找到了下面这个更妙不可言的数学表示等式,并且由他开始使用希腊字母“
”表示圆周率。之后这个符号被欧洲数学家所接受,并应用开来。
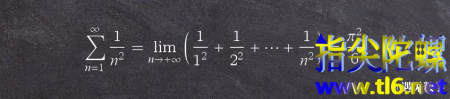
上面其实就是巴塞尔问题的准确结果,这样其实计算得也是无穷级数和。不过,真正奇妙的是所有平方数倒数之和居然与
搭上了关系。
除此之外,欧拉还在另一个漂亮的方程中用到
,即欧拉恒等式。
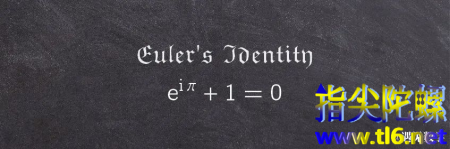
计算
的方法再改进,感谢印度数学家斯里尼瓦瑟·拉马努金给出了下面新的计算
的级数方程,其收敛速度更快。话说他在印度独立工作时就提出了许多新颖的计算
的数列,而当他远渡重洋去往剑桥所携带的一个笔记本里就有整整400页都是关于
的内容。
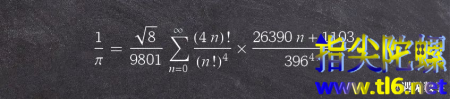
科技的进步,随着机械计算机诞生之后,数学家们就迫不及待利用这种新式工具应用莱布尼兹公式、欧拉公式和拉马努金的无穷级数来计算出
的千百万位小数。要知道之前手算
非常困难,并且容易出错。比如,数学家威廉·向克斯宣传计算出
的前707位,但遗憾的是,从527位之后他就犯了一个错误,再往后的枯燥的计算显得毫无意义。
无处不在的
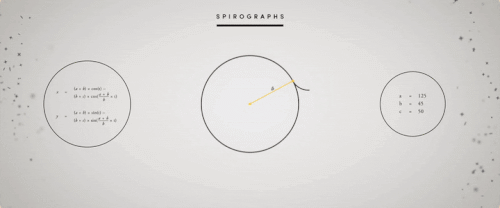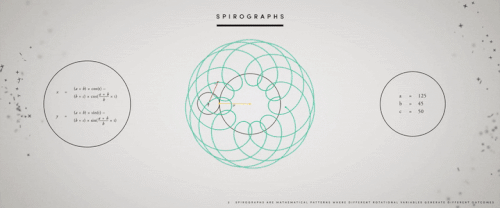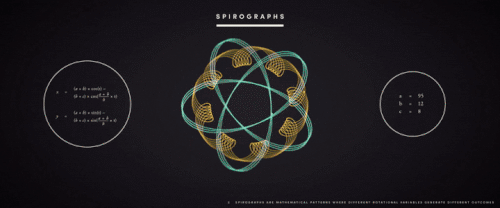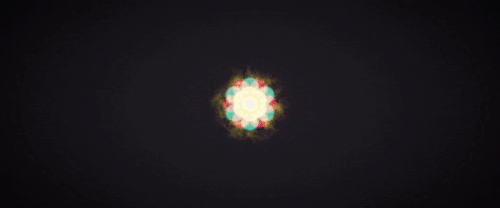
▲万花尺所画出的图案,与外图板圆圈半径、内圆图板半径及笔洞位置有相关性,其图案令人联想到万花筒
在宇宙中无处不在,也时刻存在于我们的生命中。它真的就是被编码进了宇宙一样,被用于处理行星轨道,电磁波,河流,极光,DNA结构,吉萨大金字塔等等……
如果一个科学家想要去描述宇宙的结构或者想要理清行星之间的关系,他绝对要用到
。因为任何涉及到圆或者球体的事情都与
有关。圆形存在于宇宙世界中任何一个角落,可以是小小的肥皂泡,可以是皎洁夜空中的圆月。这就解释了为什么数学在科学的所有领域中都是重要的,而
能够帮助我们去理解万事背后所蕴含的数学思想。
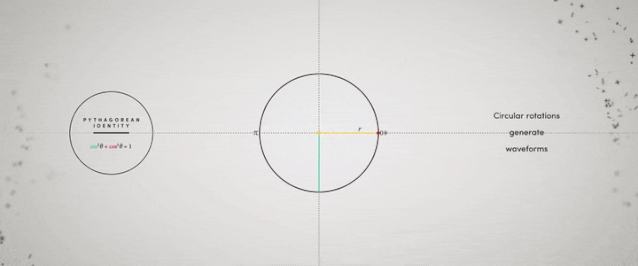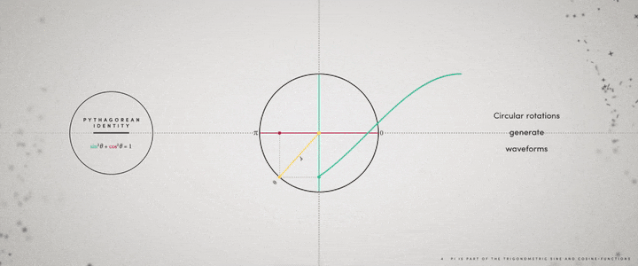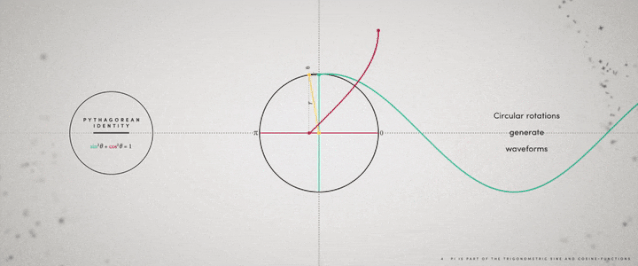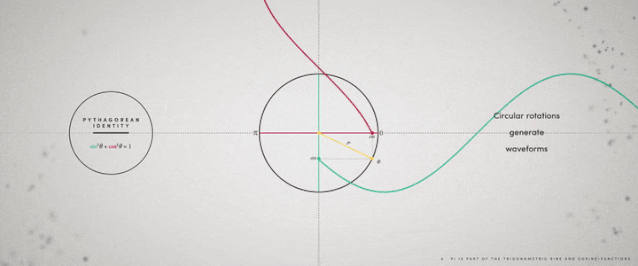
▲旋转生成正弦和余弦函数曲线河流的弯曲系数
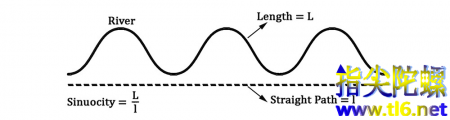
▲一条振荡曲线河流的弯曲系数
与地球上的河流有着直接联系,但如何测量呢?我们用两种不同的方法去丈量一条河的长度,假定我们知道这条河的起点和终点。首先,我们需要河流的实际长度才能知道这条河有多弯,换句话说,你从河流的起点游到它的终点的这段距离就是这条河的长度“
”;其次,我们需要知道河流起点直接到达终点的直线长度“
”,这样我们就得到了河流弯曲系数的公式,它等于
,从这个公式可以知道河流的弯曲程度。
最重要的是从这个公式里我们看出河流弯曲系数没有上限值,一条河也可以非常弯。然而,地球科学家Hans-HenrikStølum计算出了世界各地的所有河流弯曲系数的平均值是
,也就是你如果对所有河流的弯曲系数求个平均值,会得到
。

▲一条河流自1984至2012的蜿蜒变迁
关于弯曲系数还有一个有趣的事实,河流可以在某些地形作用下会变得非常弯曲,但再往后又突然变直,这样在某些范围内它的弯曲系数值会很大,但是总体求平均之后又能等于
均值。根据流体动力学,数学家们计算出的河流弯曲系数最大值约为3.5,最小值约为2.7。随着流水对河面的冲刷与侵蚀,河流愈来愈曲,最后导致河流自然截弯取直,抄近路重新变成直线,原来弯曲的河道被废弃,形成湖泊,因这种湖泊的形状恰似牛轭,故称之为牛轭湖(河迹湖)。这使得河流蜿蜒度系数会在
上下浮动。
在大自然中寻找
的身影
借助无穷级数并不是寻找
的唯一方法,在我们日常的一些很酷、有趣的实验也能得到
的近似值,其中一个叫做蒙特卡罗方法。
蒙特卡罗方法
蒙特卡罗方法是一种以概率统计理论为指导的数值计算方法。它用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
现在假定我们有一张网格型坐标纸,建立有原点的平面直角坐标系,利用介于0和1之间的数对标出坐标平面上第一象限的点,在这过程中,你会发现一些点到原点的距离小于1,一些点到原点的距离大于1,而这些点之间就是四分之一的圆周,它的面积几乎就是
/4,下图是一个有1000个点的例子。
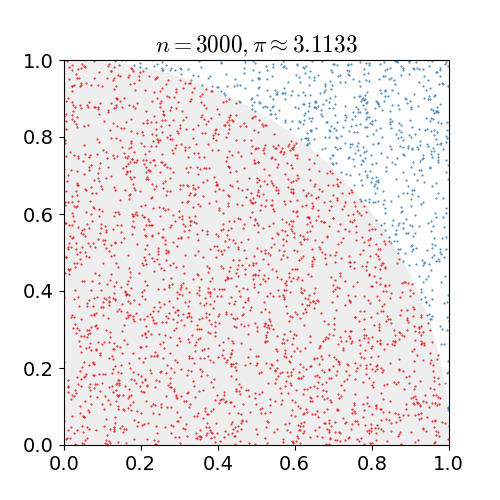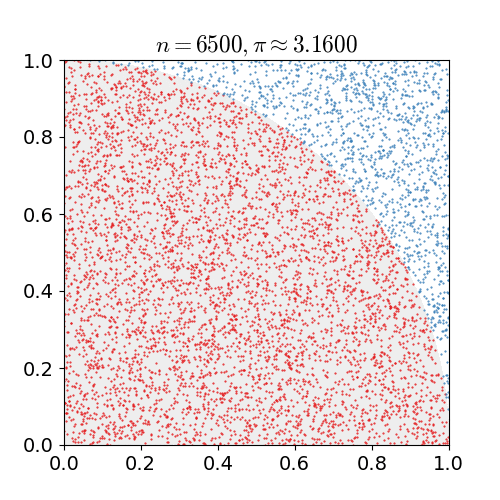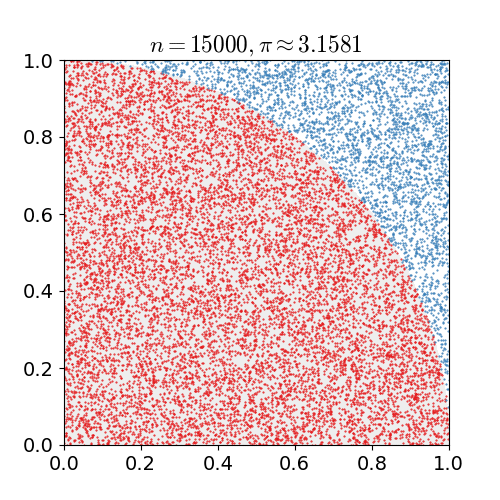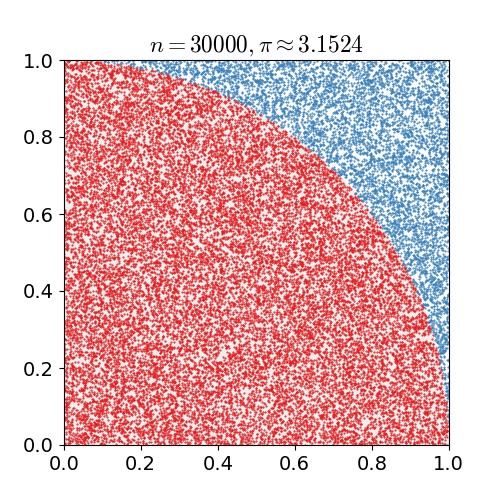
▲使用蒙特卡罗方法估算
值.放置30000个随机点后,
的估算值与真实值相差0.07%(图自维基)
布丰投针
18世纪法国法国博物学家、数学家乔治·路易斯·勒克莱尔尝试计算一个实验中某个事件的概率值。具体是这样的,他准备了一张印有多条横线的格纸,随机地向画有平行直线的纸上将针投掷若干次(针的长度小于两条横线之间的距离),然后计算针与线相交的概率。之后他用许多针做了多次重复的试验,试验结果显著,这个概率值接近
值。
这里设针的长度是l,平行线之间的距离为
,当抛
支针,其中有
支针与线相交,则有如下的公式:

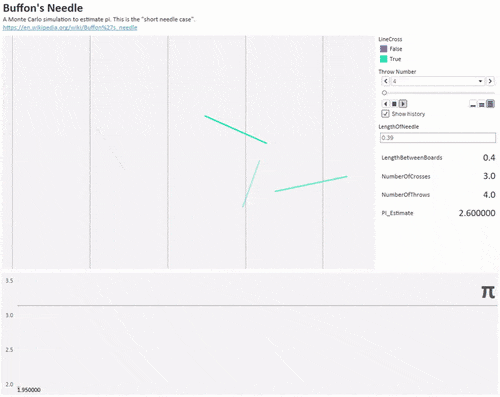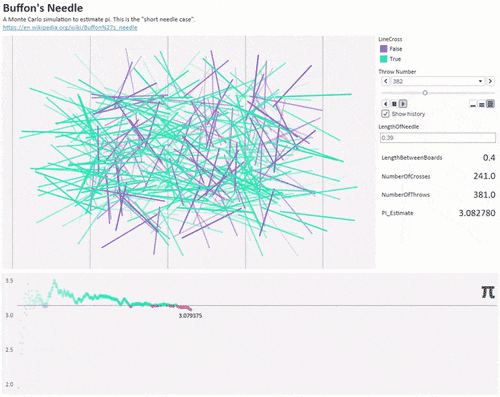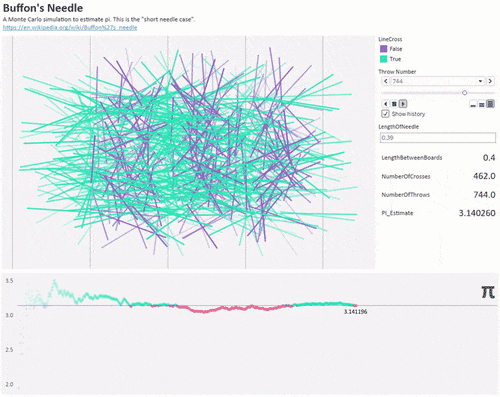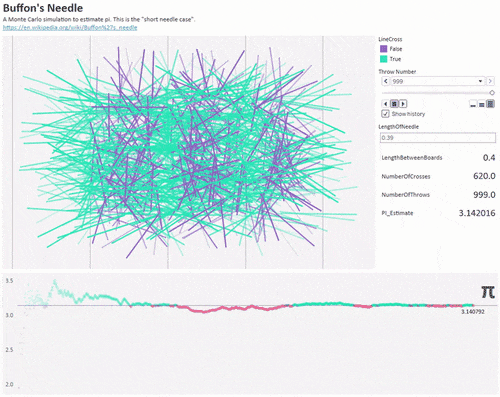
▲1000根针来估算圆周率(图自Reddit)圆周率日
人类对圆周率的研究已经有近4000年的历史了。1988年,物理学家赖瑞·萧在旧金山探险家科学博物馆举办了首次圆周率日派对庆祝活动。另外,这天也是爱因斯坦的生日,爱因斯坦还曾在这一天发表过他的广义相对论。
▲谷歌曾不止一次在圆周率日推出过相应主题涂鸦
简言之,数学其实是一门铭刻在全人类大脑里的语言,而
只是其中的一个符号。正如约翰·肯尼迪知晓月球离我们不是无限遥远,虽不容易,但人类只要努力就是能到够到达。我相信,总有一天伟大的数学家们会揭示
越来越多的秘密,与
共舞。
最后,我多么希望芬奇先生是我学生时代的老师。(-End-)