牟合方盖:圆与球的圆舞曲
浏览1562次圆与球是几何图形中最基本的两种,都具有轴对称性。实际上平面的圆形,若以任一条直径为轴旋转,就可得到一个立体的球形。 圆和球还是最实用的图形。宏大如宇宙天体,微小至原子电子,飞转的车轮,滴嗒的钟表人们的日常生活离不开圆和球,科技的进步也离不开圆和球。 就以北京...
祖暅原理牟合方盖:算个球的表面积!
浏览2330次前段时间有人问小编, 球的体积计算公式是什么? 由于长期依赖各类搜索,再加上对 睡觉 , 刷剧 , 电子竞技 等一系列新兴趣的开发,这些似曾相识的公式早被我抛诸脑后。之后再拿起笔尝试推导我才愕然发现, 基础的微积分计算法则好像也有些生疏了。 于是我开始了相关探索,半天...
牟合方盖体积公式推导
浏览1649次题目发布: 看看你的三维空间想象能力多深厚! 答案公布 解题原理牟合方盖 概念理解 详细教程步骤 Step1按照尺寸画出图示图纸,并做节点标记(红色点) Step2正方形端点画圆(圆-两点画圆) Step3切换至西南等轴侧视图 Step4三维旋转命令--3R Step5拉伸建模EXT、长度200 Step6继续拉伸建模EXT、...
牟合方盖体积怎么算?
浏览1851次我国古代数学家利用牟合方盖(如图甲)找到了球体体积的计算方法.牟合方盖是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,图乙所示的几何体是可以形成牟合方盖的一种模型,它的主视图是() 【答案】B 牟合方盖是由我国古代数学家刘徽首先发现并采用...
牟合方盖与球的体积
浏览1532次有两个直径相等的正圆柱体,它们垂直相交(互相穿过对方),那么,两者公共部分的体积怎么计算? 下图所示是由沿x轴方向的正圆柱体与沿y轴方向的正圆柱体正交后公共部分的上半部分。只画一半,因为另一半与这一半对称。图中绿色阴影是x轴方向圆柱面的一部分,蓝色阴影是y方向圆...
从"牟合方盖"品中国古代数学的辉煌
浏览1851次牟合方盖 中华文化博大精深,提到中国古代数学,不得不提牟合方盖,下面一探究竟。 笔者应公众号留言,尝试以GeoGebra做了一个牟合方盖,老师们有兴趣可以参考,也可以到文章末尾下载源文件参考,制作过程见本文最后视频. 牟合方盖效果如下: 下面我们一起来叭叭牟合方盖的历史。...
牟合方盖指的是什么?
浏览2764次牟合方盖 劳动出真知,这话一点也不假!很多人都没有见过实物的牟合方盖,哈哈,实话告诉你,铁匠师傅都知道! 冬天很冷啊,这不,小狗都受不了了! 上图小狗围着的叫做火盆,是北方过去取暖的一种方式,更多的是下面这张: 这叫火炉,请各位注意左侧烟道的拐弯处,那个结构就...
牟合方盖是什么?
浏览3366次牟合方盖是什么?相信很多人对于这个都很陌生,牟合方盖是由我国古代的数学家刘徽发现的一种用于计算球体体积的方式,他希望可以用牟合方盖来证实《九章算术》的公式有错误,但是最后也没有实现,但是牟合方盖的发现有重大的历史意义,牟合方盖是如何计算球体的体积计算方法的...
牟合方盖的定义及由来
浏览2372次一道关于高中数学三视图的题目: 有人要问,什么是牟合方盖呢? 是当一正立方体用圆柱从纵横两侧面作内切圆柱体时,两圆柱体的公共部分。刘徽在他的注中对牟合方盖有以下的描述: 取立方棋八枚,皆令立方一寸,积之为立方二寸。规之为圆囷,径二寸,高二寸。又复横规之,则其形有...
变态杀人狂魔董文语,自称“杀人者,恨社人”
浏览4531次各位老铁你们好呀 你们的东哥又来叨叨了 今儿东哥给大家说个 狠人 他是全国悬赏10万的A级通缉犯 曾连续犯下杀人奸尸案 被人称为死亡笔记的董文语 2006年3月11日至5月26日 在这 短短的两个半月时间里 董文语连续制造五起 入室抢劫强奸杀人案件 杀死6人,重伤2人 2006年3月11日凌晨 一个身影...
人吃人:60年代“杀伢儿”案,湖南澧县刘家远杀
浏览805次这起案件发生于湖南澧县,起初并未引起太多关注,随着北大法学硕士余习广关于该案的一段考证曝光,才在网络上流传开来。 刘家远出身贫寒,1948年被国民党抓壮丁,押上炮火连天的战场。 不久,他所在的部队战败,刘家远也成为解放军的俘虏,经过一番教育,转变了观念,主动帮助解...
最新复仇者纸飞机颠覆之前所有的纸飞机还能用
浏览2380次最新复仇者纸飞机颠覆之前所有的纸飞机还能用VR控制 纸飞机相信大家小时候都玩过吧,作业纸都拿来折纸飞机了。无论简单还是复杂,飞得远近,总会为我们的童年带来无穷的乐趣。童年的纸飞机,已经越来越遥远了。现在以色列 PowerUp Toys 公司与法国著名无人机公司 Parrot 联合推出的,...
巴西属于哪个洲的国家?实力仅次于美国的南美
浏览3357次作为整体实力仅次于美国的美洲国家,巴西,全称巴西联邦共和国,位于南美洲东部,北邻法属圭亚那、苏里南、圭亚那、委内瑞拉和哥伦比亚,东濒大西洋,南接巴拉圭、阿根廷和乌拉圭,西界秘鲁、玻利维亚,国土面积约851.5万平方公里(南美第1、全球第5),总人口约2.1亿,首都是巴...
朱一龙个人资料介绍“禁欲系男神”朱一龙上位
浏览422次一、 1997年,9岁的 武汉男孩 朱一龙跟艺校去朝鲜参观,爸爸担心他太小不会保管钱,就给他买了一条带拉链暗兜的内裤,往里面塞了几百块不料,待到回国,朱一龙只花了十多块钱,买的都是按摩捶、纪念币和小瓷老虎等纪念品,当做礼物送给家人。 读小学时,天生丽质的朱一龙就被老师选中,和另外两个小朋友表演《三个和尚》的短剧故事。 为此,妈妈专门用丝袜给他剪了...
“世界娱乐之都”:美国内华达州的沙漠赌城拉
浏览402次拉斯维加斯:美国内华达州的沙漠赌城,被誉为世界娱乐之都。 赌城拉斯维加斯 美国是当今世界的头号强国,美国的强大不仅仅体现在经济、军事、科技等方面,还体现在文化方面,向世界输出文化是一个国家强大的标志,美国的众多城市都是美国的文化符号。美国是一个历史很短的国家,美国的建国历史才两百多年,所以美国的城市基本都没有悠久的历史,美国的城市都是现...
明朝小冰河时期有多冷?明朝小冰河时期死了多
浏览555次三百年前的中国冬天有多冷?明清小冰河期是什么? 明朝末期曾经出现了著名的小冰河时期,也就是反常的极寒时期。 这个小冰河期,在中国历史上并不罕见,有明确记载的就有4次。 第一是商朝末年到西周初年。 当时农业种植还很落后,一亩产量往往只有几十斤小米。 农民即便辛苦劳作...
指尖陀螺_手机互动百科
浏览2882次指尖陀螺_手机互动百科指尖陀螺是一种一个轴承对称结构、可以在手指上空转的小玩具,它是由一个双向或多向的对称体作为主体,在主体中间嵌入一个轴承的设计组合,整体构成一个可平面转动的新型物品,这种物品的基本原理相似于传统陀螺,但是需要利用几个手指进行把握...
广州版雨夜屠夫连环杀手杀人王罗树标,罗树标
浏览2250次1990年2月,广州市公安局民警接到了一则报警电话,报案人称在敦和路路边发现了一位已经死亡的女性遗体。办民警接警后立即出动赶往现场进行调查,在报案人所说地点附近的一个草丛中民警发现了报案人口中的那个女性遗体。这位受害者看起来大约有25岁上下,死者面容较好,是一个漂...
指尖陀螺无聊玩具却因为无聊而兴起了指尖陀螺
浏览1976次指尖陀螺无聊玩具却因为无聊而兴起了指尖陀螺 即便是在触类旁多的VR职业中,Merge VR也能够算得上奇葩。尽管它们口口声声表示要投身于教育事业,但该公司旗下的内容和硬件明显更...
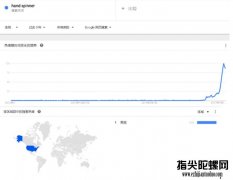
视频网站上面玩的指尖陀螺什么样子
浏览6479次视频网站上面玩的指尖陀螺什么样子?视频网站指尖陀螺图解 指尖陀螺是可以在手指上空转的小玩具,它的谷歌搜索热度显示是从 2016 年 9 月份开始飙升的,搜索热度最高的地区是美国。现在,...
视频网站上面关于指尖陀螺的视频
浏览3898次最近视频网站上面关于指尖陀螺的视频 为什么还不重视我。。。 点击播映 GIF/1710K 你以为 指尖陀螺 真的就仅仅一个减轻焦虑的小工具? 少年,别这么单纯。 指尖陀螺 ,它的本体,其实是一件具有不为人知的强壮力气的战役兵器。 在不为人知的漆黑街头,有那么一群人,关于他们来说, 指尖陀螺 即是力气的标志。 谁的 指尖陀螺 转速越快,谁即是集体里更受敬重的存在。 点...
养臭水危害及养臭水排行榜
浏览1162次20年老污师,污水处理工程师,今天来聊一聊臭水排行榜,第三位和第一位,你绝对想不到。 最近,有同学们在养臭水,从科学探索来说呢,这是一个好故事,但是,动作做错了,那可能是大事故。 我看同学们的化学实验,没有认真学啊,用鼻子对着瓶口直接吸,简直疯了。 有毒 臭水里,必不可少的一味药,就是硫化物,硫化氢中毒是发生在污水处理行业中最多的安全事故。要...
从指尖陀螺、萝卜刀到养臭水
浏览354次指尖陀螺、萝卜刀之后现在很多小学生迷上了养臭水 #养臭水正在许多学生间风靡# #别养臭水了可能会得肺炎# 等多个有味道的话题登上热搜 很多网友疑惑: 臭水是什么? 为什么要养臭水? 其实,所谓养臭水,就是学生将各种过期、废弃、腐朽的食物、液体、昆虫等收集起来, 加水后放入瓶子里养着观察,最终目的就是期待瓶身炸开,让臭味弥漫。 △网络上晒出的各色臭水 医...
从指尖陀螺到烟卡、萝卜刀、蝴蝶刀
浏览1109次指尖陀螺、烟卡、萝卜刀、蝴蝶刀这些都是最近一段时间小朋友之间非常流行的玩物。为什么说玩物而不是玩具,因为烟卡就是一个破纸片,连玩具都算不上,经常看新闻说有小孩拍烟卡把手指头都拍到骨折之类的,非常震惊,还专门问了伊森,他说至少六年级的男生们对这个是不感兴趣,但是五年级及以下的男生们看起来很痴迷。 非常庆幸伊森对这个破卡片不感兴趣,但是萝...
指尖陀螺、盘珠子、玩萝卜刀、拆盲盒、集卡片
浏览458次近日,烟卡游戏在广东、广西、湖南、海南等地小学校园中流行起来,一些学生拍烟卡上瘾,还有的已经脱离了游戏层面,升级为赌博。 在当今的校园生活中,中小学生的流行趋势犹如浪潮般一波接一波。 指尖陀螺、盘珠子、编绳子、抽盲盒、集卡这些游戏在孩子们中掀起了阵阵热潮。 面对这一现象,一个重要的问题摆在社会面前:禁止真的可行吗?山西晚报记者围绕此现象展...
从指尖陀螺到萝卜刀又到烟卡
浏览827次童年的回忆总是让人心潮澎湃。姐姐提到的小外甥沉迷于收集烟卡,让我想起了自己小时候同样沉迷于各种小游戏的时光。我们小时候,没有如今琳琅满目的电子产品和网络游戏,但我们的娱乐方式同样丰富多彩,充满了童真和乐趣。 今天和姐姐打视频,无意中姐姐说起了上小学的小外甥最近痴迷玩烟卡,走在路上还像个捡垃圾的一样低头找各种烟盒。 回想起他之前对指尖陀螺...
萝卜刀自述,小学作文
浏览2273次早上,我正在自己的国家玩,我和他们已经玩腻了,所以我准备毒害外国的孩子。 我的第一个目的地:中国。我刚到中国就名声大噪。很受学生们的喜爱,家长们也有些手痒,等学生去上学了,家长们就开始玩啦,照着自己孩子的样子嚓咔一下,我露出了一个不怀好意的笑容。 我的包装上写着:看谁不爽就刀谁一下。这是我妈妈为了我毒害更多的人而设计出来的标语。如果你一...
萝卜刀的安全隐患都有哪些?还有哪些安全隐患
浏览361次远离 萝卜刀 对危险玩具 说不! 关于玩具萝卜刀致家长的一封信 尊敬的家长朋友们: 你们好! 近期一款名为萝卜刀的新型玩具在中小学生群体中走红。该玩具是一种外形酷似胡萝卜的彩色塑料玩具刀,学生可迅速将刀甩进甩出,并进行捅刺或割喉动作。由于该玩具本身具有攻击性,存在一定的安全隐患,又会形成心理暗示,激发孩子暴力倾向,对未成年人安全健康成长产生不...
“指尖陀螺”“萝卜刀”后,“注射器”又来了
浏览365次近日,陕西安康汉阴县实验小学 有小学生在学校对面文具店 买到带针头的注射器 家长发现后愤怒不已 文具店售卖的带针头的注射器(媒体报道截图) 文具店向小学生出售注射器 当地市监局介入 据北京广播电视台《法治进行时》社交账号发布的视频显示有家长拿着有针头的注射器怒斥文具店店主 这是违禁品 只有医院才会使用 带针头的东西 为何要卖给这些小孩? 据了解,涉事...