郭守敬的主要贡献是什么方面 1.数学:郭守敬参与制定的《授时历》除了在天文数据上的进步之外,在计算方法方面也有重大的创造和革新。 2.光学:郭守敬在创造的景符、仰仪等天文仪器中反复运用了针孔成象原理,这在中国光学史上也是比较突出的成就,体现了中国古代较高的光学知识...
郭守敬的主要贡献是什么方面?科学家郭守敬介绍
浏览1512次郭守敬出生于1231年,死于1316年,郭守敬字若思,是河北邢台人,郭守敬是元代著名的天文学家、仪器制造家、水利专家和数学家。 到了1276年年,元朝令郭守敬和王恂率南北日官数人负责新历的测验和推算工作。 为了完成这项工作,郭守敬研制了许多新的天文仪器。 公元1279年时,郭守敬...
郭守敬的主要贡献是什么方面?京杭大运河主要功臣
浏览1333次1、郭守敬参与制定的《授时历》。除了在天文数据上的进步之外,在计算方法方面也有重大的创造和革新。 2、郭守敬在创造的景符、仰仪等天文仪器中反复运用了针孔成象原理。这在中国光学史上也是比较突出的成就,体现了中国古代较高的光学知识应用能力。 3、郭守敬运用他改进、创...
郭守敬是我国的历史名人,在很多方面都有很深的造诣,现在有很多人很崇拜郭守敬,但是他们并不知道郭守敬的主要贡献是什么,只是听别人提起郭守敬比较厉害,所以就跟着喜欢郭守敬,其实,喜欢,崇拜这样的历史名人是件好事,但是也不能太过盲目,下面,指尖陀螺网就来为大家简...
郭守敬的主要贡献是什么方面?郭守敬主要贡献介绍
浏览1525次郭守敬的主要贡献在天文学、地理学、水利学、数学、光学这五个方面。郭守敬,字若思,今河北省邢台市信都区人,郭守敬是元朝水利工程专家、天文学家、数学家,主要作品有《授时历》、《立成》、《推步》等。 郭守敬的主要贡献是什么方面 在天文学方面,郭守敬运用自己改造的天...
郭守敬的主要贡献是什么方面?
浏览1331次郭守敬(1231~1316年),是元代著名的天文学家、数学家、水利工程专家,在天文历法、水利工程、数学和测量等方面取得了卓越的成就。特别是郭守敬在主持航道疏通、黄河治理和运河修贯等水利工程中,首创海拔概念并运用于水利工程测量,主持进行了天文测量仪器创制和大规模的天文...
郭守敬的主要贡献是什么方面?集“观象授时”之大成
浏览1152次生活背景生于13世纪的郭守敬(12311316)对中国古代科学的贡献与张衡不相上下。 1231年,郭守敬出生在河北邢台。 当时的社会可以用战乱不断一词形容。 邢台本来属于宋朝,建炎二年(1128年)被金人夺去,1220年,又落入蒙古人手中。 1234年蒙古人灭金,1279年,南宋全境沦陷。 郭守敬并不...
郭守敬的主要贡献是什么方面?郭守敬主要贡献
浏览1689次郭守敬在天文、地理、水利和数学等方面都有巨大贡献。著有《推步》、《立成》等十四种天文历法著作,制订出了通行三百六十多年的《授时历》,郭守敬还改制、发明了简仪、高表等十二种新仪器。至元元年(1264年),郭守敬奉命修浚西夏境内的古渠,更立闸堰,使当地农田得到灌溉...
郭守敬的主要贡献是什么方面
浏览4443次郭守敬在我国古代科学技术史上贡献巨大,被誉为元朝科学第一人,郭守敬一生的贡献主要在于天文学,郭守敬在天文方面有以下几个贡献。 1、参与制定了《授时历》。此书不但在天文数据上有巨大进步,而且在天文学的计算方法方面也有重大的创造和革新。 2、创造景符、仰仪等天文仪...
-
共1页/9条
芝麻女孩玉米男孩图片
浏览2744次听十宗罪的时候听到有关芝麻女孩儿的故事,当时感觉很害怕,晚上吃火龙果,切开之后就想到了,怕的不行。后来好多了,只是偶尔会想到。 昨晚看漫画,不经意看到一则,其实内容并不吓人,只是片头提到,密集恐惧症者小心慎入,之后我就在意了,一夜... 起因,是因为听十宗罪的时...
乐山大佛的传说:四川乐山大佛胸口旁边,发现密
浏览477次关于四川乐山大佛,有诗人李祚忠的一首五绝为证: 头大与山高,足宽踏浪涛。千年仍未老,静坐看朝朝! ,李祚忠的这首诗,将乐山大佛的特点,展示得玲离尽致。头大与山高,足宽踏浪涛。,坊间也有一句俗语来形容乐山大佛,更加贴切,叫 山是一尊佛,佛是一座山 。 虽然叫乐山大...
七夕节不知道送男朋友什么礼物,试试指尖陀螺
浏览3759次七夕节不知道送男朋友什么礼物,试试指尖陀螺相对于女生而言,男人收到礼物的兴奋度是女人的一百倍,因为男孩子平时真的很少会想到真的有人会送礼喔。 七夕送男朋友什么礼物好 ?小编问了很多男生,大致分为经济型、象征型、实用型、体验型吧哈哈,都是男生的心声,看完觉得有...
戴套100种啪法图片有图片超详细
浏览37357次在人们的日常性生活中,总会有放荡不羁的时候,讨厌被束缚的避孕措施,但是又不想让孩子过早的出现,这个时候人们通常就会选择吃避孕药这种方法,但是人们只知道避孕药可以起到避孕效果,人们其实不了解,避孕药也是有一些禁忌和副作用的,长期的服用避孕药的话会对女性的身体...
《终结者2》:陀螺仪瞄准功能的使用攻略
浏览2991次《终结者2》:陀螺仪瞄准功能的使用攻略 终结者2审判日2月28日新增了陀螺仪瞄准功用,这是一个可以进步射击精准度十分有用的功用,下面就跟着小编一起来了解一下,终结者2陀螺仪是什么?有什么用?怎样用? 陀螺仪有什么用? 陀螺仪功用是在瞄按时协助微调瞄准,让你的射击愈加精...
盘点“妈宝男”明星背后的大瓜!
浏览506次一年来,我们吃了不少瓜,不少明星一夜之间塌房,有一个现象值得特别关注,那就是 塌房的男星里有不少妈宝男 。 那么,为毛妈宝男很多都能成为大明星呢? 所有的妈宝男母子之间,必定十分亲密,母子连心,母子关系看起来甜得发腻,乍一看,令人无比羡慕。在母子关系中,妈宝男一定是个唯命是从的小乖乖,对母亲言听计从,还总能想方设法哄母亲开心 哄母亲开心最好...
清朝女天文学家王贞仪,在国际上赫赫有名,国
浏览670次国际知名的《自然》(Nature)网站在关于2019年度激励科学与创新科学研究奖提名的宣传片中,登出了一位名为 王贞仪 的 中国清朝女科学家 ,作为当前女性科学家的前辈代表。 吐槽一下Nature的视频制作水平:随便找了张不相关的国画仕女图,还把文案诗句谁言儿女不英雄的谁字吞了 在Na...
能飞9000000米的纸飞机怎么折图片图解
浏览38778次折纸飞机是没给人孩童时期一定都玩过的一种游戏。小伙伴之间不仅要比较谁的飞机飞的远,更要折出样式新奇、好看的纸飞机。你知道吗,不仅是中国,全世界都在玩折纸飞机游戏,甚至有些经典折法可是全世界通用的。 小编在网上搜罗了四类经典的纸飞机折法,看看有没有你小时候用...
纸指尖陀螺制作图解
浏览3650次纸指尖陀螺制作图解 今天小编去说故事研习进修 刚好今天的研习老师玉米妈妈教了一个很棒的折纸玩具-纸陀螺 小编觉得很不错 可以让孩子自己动手做纸陀螺也不错 训练一下手部精细...
查尔斯·曼森:创邪教,杀孕妇,至今追随者无数
浏览1587次11月19月,美国历史上最著名的杀人魔王查尔斯曼森(CharlesManson)在监狱中去世,终年83岁。 查尔斯曼森 他建立了臭名昭著的邪教组织曼森家族; 他曾指挥杀害波兰斯基正在怀孕8个月的妻子莎朗泰特; 她是7桩连环谋杀案的始作俑者; 他激发了无数的文学艺术创作、吸引了一波又一波追随者...
视频网站上面玩的指尖陀螺什么样子
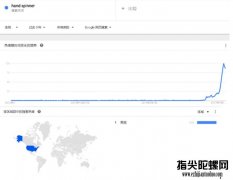
浏览6418次视频网站上面玩的指尖陀螺什么样子?视频网站指尖陀螺图解 指尖陀螺是可以在手指上空转的小玩具,它的谷歌搜索热度显示是从 2016 年 9 月份开始飙升的,搜索热度最高的地区是美国。现在,...
视频网站上面关于指尖陀螺的视频
浏览3871次最近视频网站上面关于指尖陀螺的视频 为什么还不重视我。。。 点击播映 GIF/1710K 你以为 指尖陀螺 真的就仅仅一个减轻焦虑的小工具? 少年,别这么单纯。 指尖陀螺 ,它的本体,其实是一件具有不为人知的强壮力气的战役兵器。 在不为人知的漆黑街头,有那么一群人,关于他们来说, 指尖陀螺 即是力气的标志。 谁的 指尖陀螺 转速越快,谁即是集体里更受敬重的存在。 点...
养臭水危害及养臭水排行榜
浏览1139次20年老污师,污水处理工程师,今天来聊一聊臭水排行榜,第三位和第一位,你绝对想不到。 最近,有同学们在养臭水,从科学探索来说呢,这是一个好故事,但是,动作做错了,那可能是大事故。 我看同学们的化学实验,没有认真学啊,用鼻子对着瓶口直接吸,简直疯了。 有毒 臭水里,必不可少的一味药,就是硫化物,硫化氢中毒是发生在污水处理行业中最多的安全事故。要...
从指尖陀螺、萝卜刀到养臭水
浏览335次指尖陀螺、萝卜刀之后现在很多小学生迷上了养臭水 #养臭水正在许多学生间风靡# #别养臭水了可能会得肺炎# 等多个有味道的话题登上热搜 很多网友疑惑: 臭水是什么? 为什么要养臭水? 其实,所谓养臭水,就是学生将各种过期、废弃、腐朽的食物、液体、昆虫等收集起来, 加水后放入瓶子里养着观察,最终目的就是期待瓶身炸开,让臭味弥漫。 △网络上晒出的各色臭水 医...
从指尖陀螺到烟卡、萝卜刀、蝴蝶刀
浏览1082次指尖陀螺、烟卡、萝卜刀、蝴蝶刀这些都是最近一段时间小朋友之间非常流行的玩物。为什么说玩物而不是玩具,因为烟卡就是一个破纸片,连玩具都算不上,经常看新闻说有小孩拍烟卡把手指头都拍到骨折之类的,非常震惊,还专门问了伊森,他说至少六年级的男生们对这个是不感兴趣,但是五年级及以下的男生们看起来很痴迷。 非常庆幸伊森对这个破卡片不感兴趣,但是萝...
指尖陀螺、盘珠子、玩萝卜刀、拆盲盒、集卡片
浏览440次近日,烟卡游戏在广东、广西、湖南、海南等地小学校园中流行起来,一些学生拍烟卡上瘾,还有的已经脱离了游戏层面,升级为赌博。 在当今的校园生活中,中小学生的流行趋势犹如浪潮般一波接一波。 指尖陀螺、盘珠子、编绳子、抽盲盒、集卡这些游戏在孩子们中掀起了阵阵热潮。 面对这一现象,一个重要的问题摆在社会面前:禁止真的可行吗?山西晚报记者围绕此现象展...
从指尖陀螺到萝卜刀又到烟卡
浏览807次童年的回忆总是让人心潮澎湃。姐姐提到的小外甥沉迷于收集烟卡,让我想起了自己小时候同样沉迷于各种小游戏的时光。我们小时候,没有如今琳琅满目的电子产品和网络游戏,但我们的娱乐方式同样丰富多彩,充满了童真和乐趣。 今天和姐姐打视频,无意中姐姐说起了上小学的小外甥最近痴迷玩烟卡,走在路上还像个捡垃圾的一样低头找各种烟盒。 回想起他之前对指尖陀螺...
萝卜刀自述,小学作文
浏览2251次早上,我正在自己的国家玩,我和他们已经玩腻了,所以我准备毒害外国的孩子。 我的第一个目的地:中国。我刚到中国就名声大噪。很受学生们的喜爱,家长们也有些手痒,等学生去上学了,家长们就开始玩啦,照着自己孩子的样子嚓咔一下,我露出了一个不怀好意的笑容。 我的包装上写着:看谁不爽就刀谁一下。这是我妈妈为了我毒害更多的人而设计出来的标语。如果你一...
萝卜刀的安全隐患都有哪些?还有哪些安全隐患
浏览341次远离 萝卜刀 对危险玩具 说不! 关于玩具萝卜刀致家长的一封信 尊敬的家长朋友们: 你们好! 近期一款名为萝卜刀的新型玩具在中小学生群体中走红。该玩具是一种外形酷似胡萝卜的彩色塑料玩具刀,学生可迅速将刀甩进甩出,并进行捅刺或割喉动作。由于该玩具本身具有攻击性,存在一定的安全隐患,又会形成心理暗示,激发孩子暴力倾向,对未成年人安全健康成长产生不...
“指尖陀螺”“萝卜刀”后,“注射器”又来了
浏览345次近日,陕西安康汉阴县实验小学 有小学生在学校对面文具店 买到带针头的注射器 家长发现后愤怒不已 文具店售卖的带针头的注射器(媒体报道截图) 文具店向小学生出售注射器 当地市监局介入 据北京广播电视台《法治进行时》社交账号发布的视频显示有家长拿着有针头的注射器怒斥文具店店主 这是违禁品 只有医院才会使用 带针头的东西 为何要卖给这些小孩? 据了解,涉事...