1月3日和1月6日的两期(封面上是第279和280号)分别讲了两种空间密铺问题:
①《有关正八面体、正四面体的有趣问题》
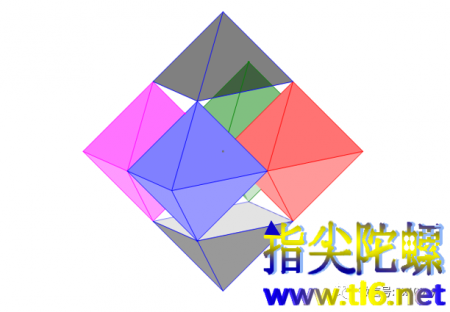
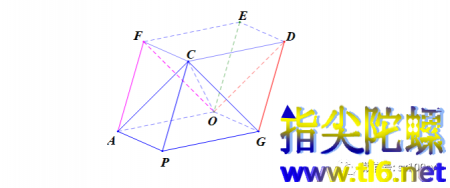
②《正四面体与截角四面体可以铺满空间》
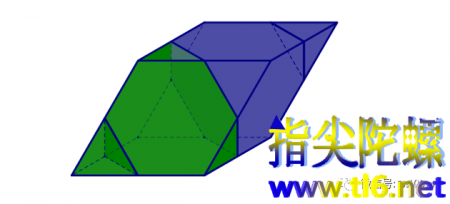
以上两期的链接在文后。
我们上期说过,有五种用柏拉图体和(或)阿基米德体铺满整个空间的方式。除上面的两种外,最简单的那种我们没有必要单独用一篇来讲,那就是由正方体铺满整个空间。还剩下两种,今天先讲一种,即如何用正八面体和截半八面体一同填充整个空间。我们还是一点点地引导着您向着正确的方向迈进。
(1)首先,下图是可以做到的。
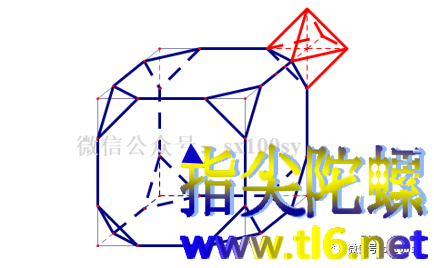
上面是把一个正方体的八个角都切去相同的正三棱锥,所得是一个叫做截角正方体的阿基米德体(注意,截的时候,要使得截痕长度与棱中剩余长度相等)。再在每个切割面上粘贴上一个正八面体。用这种阿基米德体与正多面体的组合,是可以密铺整个空间的。这只要看一下下图即可以懂得。三个方向都可以扩充。所以也就可以扩充到整个空间。
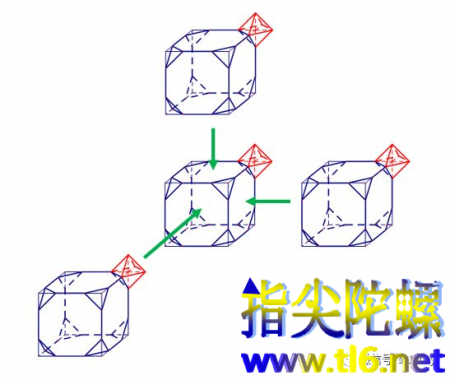
其实,就是在正方体密铺的基础上,在其相交顶点处(类似空间直角坐标系八个卦限相交于原点),挖去以这个顶点为中心的一个正八面体。这个正八面体分别由相邻的八个正方体各贡献的一个正三棱锥拼成。
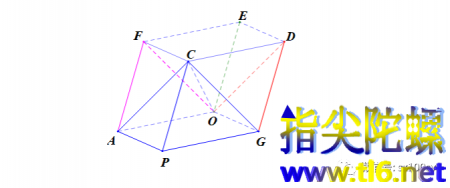
(2)我们研究一下棱的情况。可以考察一条棱连接着几种多面体,也可以考察一条棱连接着几种正多边形面。比如上图中,切割产生的棱连接着一个正八面体和两个截角正方体。也可以说,切割产生的棱连接着两个正三角形面和一个正八边形面。但我们再观察截角正方体的另一种棱,它是原正方体棱被截后剩下的一段,它不与正八面体有棱相连,而是与其他三个截角正方体相连。也可以说,这条棱与四个正八边形面相连。所以,存在两种不一样的棱。但是,若切割面截到棱的中点,则原来正方体的棱就消失了。这时的截角正方体就变成下面的样子,它叫做截半正方体。

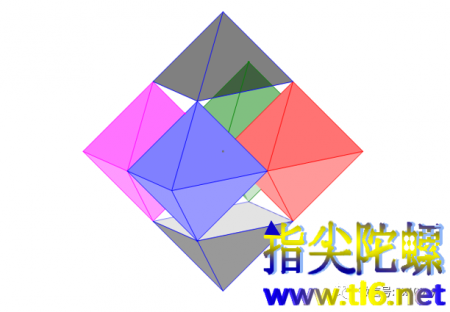
您若仔细的话,可能发现标题中是“截半八面体”,是的,截半正方体与截半八面体是同一种阿基米德体。见下图。可以看出,从橙色正八面体棱中点截掉六个角(四面角),与从粉色正方体也从中点处截掉八个角(三面角),结果一样,就是上图这个截半正方体。

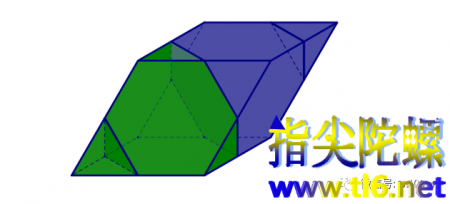
那么,既然前面由一个截角正方体与一个正八面体构成的组合体可以密铺整个空间,那么,由截角正方体的极限情况——截半正面体与正八面体构成的组合体同样地可以密铺整个空间。并且所有的棱就只有一种情况(连接着的正多面体完全一样,连接着的正多边形也完全一样)。我们就是需要这样一种全部棱都一样的组合体。如下图所示。(是不是像个斜放着的小瓶子?)

可以想像上图:一个正八面体由八个截半正方体围绕着,它们之间没有任意空隙。一个截半正方体由八个正八面体和六个与自己相同的截半正方体围绕着,它们之间没有空隙。两种围绕或缠绕方式互相交错,可以无空隙无重叠地铺满整个空间。
分别讲了两种空间密铺问题:
①《有关正八面体、正四面体的有趣问题》
②《正四面体与截角四面体可以铺满空间》
以上两期的链接在文后。
我们上期说过,有五种用柏拉图体和(或)阿基米德体铺满整个空间的方式。除上面的两种外,最简单的那种我们没有必要单独用一篇来讲,那就是由正方体铺满整个空间。还剩下两种,今天先讲一种,即如何用正八面体和截半八面体一同填充整个空间。我们还是一点点地引导着您向着正确的方向迈进。
(1)首先,下图是可以做到的。
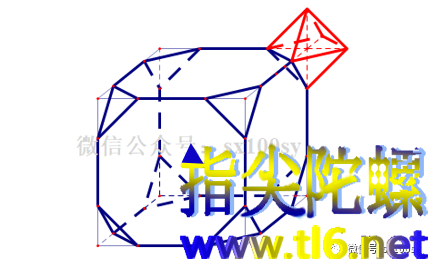
上面是把一个正方体的八个角都切去相同的正三棱锥,所得是一个叫做截角正方体的阿基米德体(注意,截的时候,要使得截痕长度与棱中剩余长度相等)。再在每个切割面上粘贴上一个正八面体。用这种阿基米德体与正多面体的组合,是可以密铺整个空间的。这只要看一下下图即可以懂得。三个方向都可以扩充。所以也就可以扩充到整个空间。
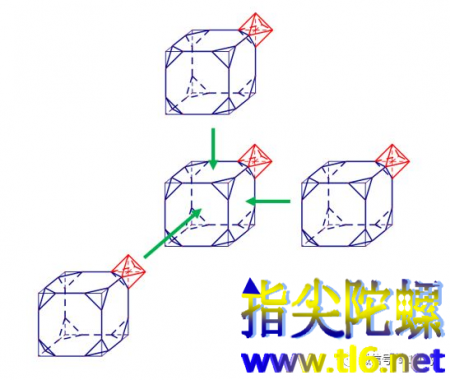
其实,就是在正方体密铺的基础上,在其相交顶点处(类似空间直角坐标系八个卦限相交于原点),挖去以这个顶点为中心的一个正八面体。这个正八面体分别由相邻的八个正方体各贡献的一个正三棱锥拼成。
(2)我们研究一下棱的情况。可以考察一条棱连接着几种多面体,也可以考察一条棱连接着几种正多边形面。比如上图中,切割产生的棱连接着一个正八面体和两个截角正方体。也可以说,切割产生的棱连接着两个正三角形面和一个正八边形面。但我们再观察截角正方体的另一种棱,它是原正方体棱被截后剩下的一段,它不与正八面体有棱相连,而是与其他三个截角正方体相连。也可以说,这条棱与四个正八边形面相连。所以,存在两种不一样的棱。但是,若切割面截到棱的中点,则原来正方体的棱就消失了。这时的截角正方体就变成下面的样子,它叫做截半正方体。

您若仔细的话,可能发现标题中是“截半八面体”,是的,截半正方体与截半八面体是同一种阿基米德体。见下图。可以看出,从橙色正八面体棱中点截掉六个角(四面角),与从粉色正方体也从中点处截掉八个角(三面角),结果一样,就是上图这个截半正方体。

那么,既然前面由一个截角正方体与一个正八面体构成的组合体可以密铺整个空间,那么,由截角正方体的极限情况——截半正面体与正八面体构成的组合体同样地可以密铺整个空间。并且所有的棱就只有一种情况(连接着的正多面体完全一样,连接着的正多边形也完全一样)。我们就是需要这样一种全部棱都一样的组合体。如下图所示。(是不是像个斜放着的小瓶子?)

可以想像上图:一个正八面体由八个截半正方体围绕着,它们之间没有任意空隙。一个截半正方体由八个正八面体和六个与自己相同的截半正方体围绕着,它们之间没有空隙。两种围绕或缠绕方式互相交错,可以无空隙无重叠地铺满整个空间。



















