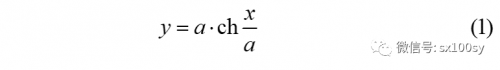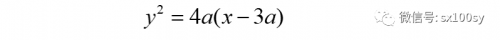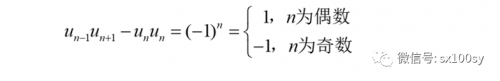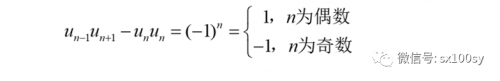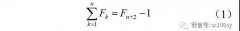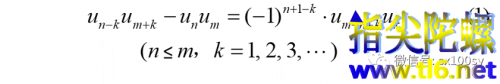缺8数
(1)先给出后面要用到的塞瓦定理。 塞瓦定理 :三角形ABC中,点D、E、F分别位于边BC、CA、AB上。那么,三条塞瓦线AD、BE、CF共点的充要条件是: (2)本期介绍 Gergonne点 。设三角形的内切圆与三条边相切之点分别为D、E、F(注意,这里的D、E、F三个点不一定是角平分线与对边的交点)。下面简单证明三条塞瓦线AD、BE、CF共点,这个点叫做Gergonne点(下图中点G)。(注意,点G与内心...
帕斯卡原理定律及其各种变化情况
浏览次今天讲对偶的帕斯卡定理,读懂每一幅图。 一、椭圆情况 1-1ABCDEF为椭圆内接六边形。 相对之边AB与DE(无C和F)相交于点X,BC与EF(无D和A)相交于点Y,CD与FA(无E和B)相交于点Z。 那么X、Y、Z三点共线。 如下图所示。 (图中六边形看上去其点A远离其他五个点,不够任意,这是为了使X、Y、Z能够全部显示在图中。 若是任意,就有可能X、Y或Z跑得很远,不利于图示。 ) 1-2ABCDEF不一定是上图那...
渐近线互相垂直的双曲线叫做等轴双曲线。若我们以x轴和y轴为渐近线,那么,等轴双曲线的方程就是xy=k(常数)。从函数的角度看,它就是反比例函数y=k/x。 取k=1,我们在直角坐标系中画出反比例函数y=1/x的图像,如下图所示。在等轴双曲线上任取三个点A、B、C。以三个点为顶点作一个三角形ABC。如下图所示。 作这个三角形的垂心P。我们发现,这个垂心P正好位于双曲线上。 下图...
第4种方法:阿波罗尼圆法 点A和B被点C和D调和分割,设点C已知,它位于线段AB之上,且不妨设点C与点B较近。我们要求点D,使得AC:BC=AD:BD。所谓阿波罗尼圆,就是指到两个定点距离的比值为常数k的点的轨迹。显然,阿波罗尼圆与直线AB的两个交点一定把AB调和分割。现在,点C已知,则比值AC:BC就是确定的了,即AC:BC=k。所以,我们只要作出到点A和B的距离的比值为AC:BC的阿波罗尼...
相交圆法 如下图所示,点A和B位于一条直线上,点C位于点A和B之间,且离点B较近一些。我们要找到一点D,使得点C和D调和分割点A和B。 今天的方法姑且叫做相交圆法,因为我们将从下面作图中看到有两个相交的圆起到重要作用。如下图所示。分别过点A和B,在直线AB同侧作两条与直线AB垂直的线段AO₁和BO₂,并且要使两条垂线段一长一短,姑且让AO₁BO₂。分别以点O₁和O₂为圆心...
用笛沙格对合定理证明坎迪定理
浏览次最近几期都讲到笛沙格对合定理。上上期我们讲了用笛沙格对合定理证明蝴蝶定理。蝴蝶定理的推广形式就是所谓的坎迪(Candy)定理。以前我讲过坎迪定理,给出了证明(见文后链接),但证明过程比较复杂。今天我给出用笛沙格对合定理证明坎迪定理,非常简洁和有效,正像我们之前用它证明蝴蝶定理那样简洁、有效。 先给出 坎迪定理 本身: 有一个圆O,任取一条弦AB。在弦...
笛沙格对合定理与完全四边形
浏览次今天讲笛沙格对合定理与完全四边形的关系。很有意思! (1) 笛沙格对合定理 一条直线截圆锥曲线于点对(S,S),截圆锥曲线的内接四边形的三组对边分别于点对(A,A),(B,B)及(C,C),那么,这四个点对位于同一个对合中。 注:我们用同一大写字母一个不带撇,一个带撇表示点对,比如(A,A)。另外,上图中,四边形PQRT的三组对边分别是QR与PT,PR与QT,PQ与RT。 (2)笛沙格对合定理...
用笛沙格对合定理证明蝴蝶定理
浏览次今天我们用 笛沙格对合定理 来证明蝴蝶定理。这个证明方法简洁、有效。笛沙格对合定理是一个很难理解的定理,属于射影几何。我们今天给出这个定理,并对其进行一些说明,但不证明。然后,蝴蝶定理的证明反就极为简洁、有效。 笛沙格对合定理 一条直线截一条圆锥曲线于点对(S,S),截圆锥曲线的内接四边形的三组对边分别于点对(A,A),(B,B)及(C,C),那么,这四个点对...
(1)圆锥曲线的内与外。如下图所示,阴影区城为内。 (2)在双曲线外一点向双曲线可以引两条切线。若这点位于双曲线对称中心,则两条切线就是双曲线的两条渐近线。所以,从非对称中心一点所引两条切线与两条渐近线,可以看成四条切线。这四条切线可以构成双曲线的一个外切四边形。 具体来说,如上图所示,直线PQ与双曲线的左支相切,直线PQ也与双曲线左支相切。点P和Q是...
范数是什么?Norm和范数的故事
浏览次范数翻译自英语norm,是一个数学术语。其功能相当于是矩阵(或向量)的大小。 一、什么是范数 数学分析喜欢比较大小多少(和人喜欢攀比差不多),但矩阵所含元素往往不止一个(等于一个便是数,可以不用玩矩阵)。两个矩阵之间有时也要比大小。如果逐个元素去比,一方面得不到大小的确切结论,另一方这样比有没有物理意义和工程意义。范数是从矩阵元素算出一个数来(算的方...
古鲁金第二定理
浏览次今天讲古鲁金第二定理。 上一期所讲的古鲁金定理可以称为第一定理。 第一定理是讲旋转面面积与旋转曲线长度及曲线质心之间的关系,而第二定理则讲旋转体体积与旋转区域面积及旋转区域质心之间的关系,维度升高一维。 两个定理的叙述类似。 上一期的古鲁金第一定理是说: 古鲁金(P.Guldin) 第 一 定理 :一条平面曲线绕同平面内一条不穿过它的轴旋转一周所得曲面的面积...
拓扑游戏
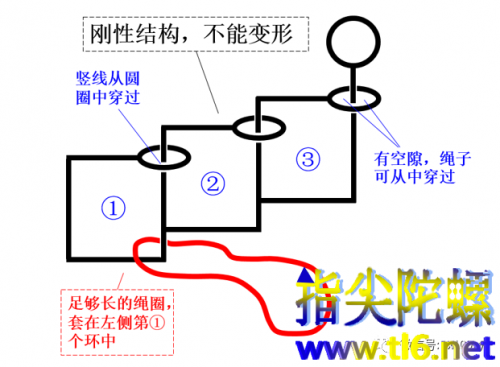
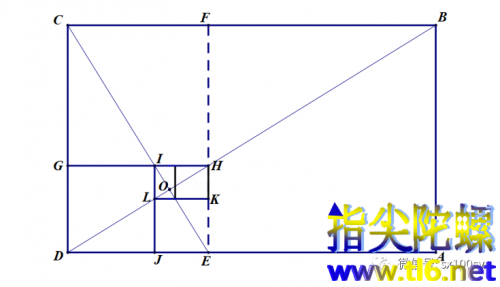
浏览次今天介绍一个拓扑学小游戏,锻炼你的空间想像力。如下图所示,是一个刚性框架。红色绳子与第①个圈套在一起(绳子是无法直接取下来的)。但结构中的三个画成椭圆形状的圆圈,与在其中穿过的直杆之间留有空隙,足够绳子穿过。那么,我们如何在既不剪断框架也不剪断绳子的前提下,把绳子从框架上取出来? 上图中的文字标明了一些条件。建议最好不要真的找来或制作...
悬链线方程的推导过程、求解及应用
浏览次今天讲一讲悬链线。把一根质量分布均匀的链子或软绳的两端系在等高的两个点上(其实不等高也不影响),则链子或软绳自然弯曲而成的曲线就是 悬链线 。很早以前人们认为悬链线是抛物线,因为看上去确实很像。但后来物理学家和数学家都证明了它不是抛物线。根据力学原理分析悬链或软绳的受力,可以得出悬链线的方程是: 其中涉及 双曲余弦 : 类似地,还有双曲正弦、...
伯努利双纽线
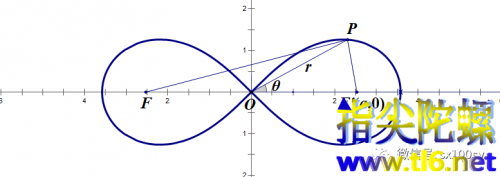
浏览次(1) 起源 。我们熟悉的椭圆是这样定义的:到两个定点的距离之和等于定长的点的轨迹。这里定长2a必须大于两定点间距离2c。雅各伯努利仿照椭圆的定义,稍做改动,发现了双纽线。他是这样定义双纽线的:设两定点F、F之间距离为2a,则到两定点距离之积为定值a的点的轨迹就叫做双纽线。双纽线的图形如下图所示,它的形状像个横着的8,也像是无穷符号。 (2) 方程的推导...
史留斯蚌线(含蔓叶线)
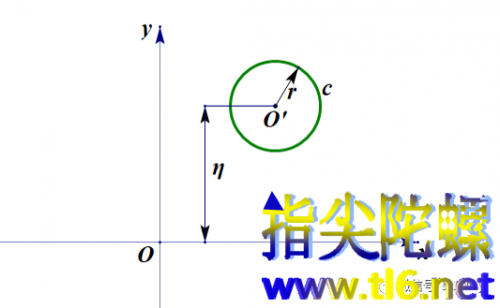
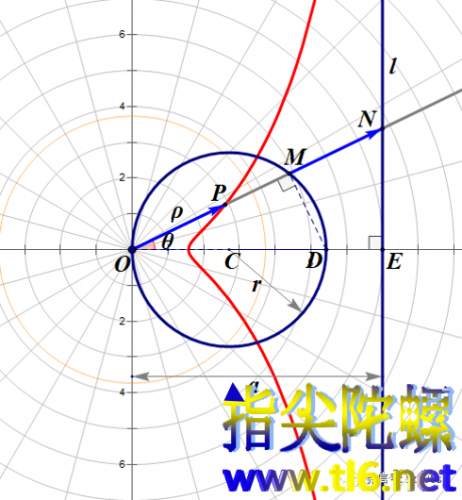
浏览次史留斯蚌线及它们与圆锥曲线之间的关系。 史留斯蚌线是这样做出来的:有一个半径为r的圆C,取一条直径OD(不妨置于水平)。还有一条直线l与直径OD垂直。直线l与圆心的距离可以变化,有相离、相切和相交三种关系。以下图相离情况为例加以说明。 以点O为极点,OD所在直线为极轴。在直线l上取一动点N,作射线ON。ON与圆交于点M。作向量MN(注意,这里取向量,是为了有方向...
麦克劳林三等分角曲线
浏览次今天简单讲一下麦克劳林三等分角曲线,及它是如何做到三等分一个角的。 (1)作抛物线: (2)在抛物线上任取一点P。作点P处抛物线的切线m。从点O作切线m的垂线,垂足为M。 (3)让点P在抛物线上运动,那么,垂足M的运动轨迹就是所谓的麦克劳林三等分角曲线。(有关垂足曲线的知识,在前两三期的内容中有过介绍。)麦克劳林三等分角曲线见下图中的红色曲线。(注意,...
对数螺线
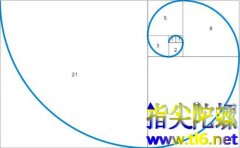
浏览次今天简单介绍一下对数螺线及其绘制方法。 还有一些与对数螺线非常接近的螺线。 首先讲一下黄金矩形。 宽与长的比值等于黄金比0.618的矩形称为黄金矩形。 黄金矩形的一个特点是,沿着与短边平行的方向,从黄金矩形中一刀切掉一个边长等于宽的正方形,所剩的图形是一个与原来矩形相似的黄金矩形。 这一过程可以无限地进行下去。 并且,如果按照一定的顺序有规律地切割...
超静定与瞬变体系有没有关系?
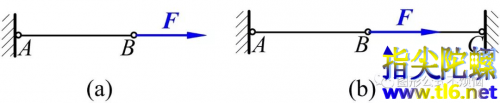
浏览次一、力学模型的视角 超静定这个词汇在理论力学和材料力学中提的多,而瞬变体系则在结构力学中谈的比较多,那么这二者有没有联系呢? 图1 看图1(a)中AB(本文所讨论的杆件均为不计重量的轻杆)。按认知习惯,对这种问题,只讨论沿杆方向的外加载荷(图中 F ),而不讨论垂直于杆的载荷。此时AB的内力是确定的。 图1(b)在图1(a)的基础上添加了一根水平杆BC【为了简洁(但不失概念准...
斐波那契数列与音乐节拍
浏览次以前讲过很多例子,它们的模型都是斐波那契数列。今天再讲一个,我们一起来看看是怎么回事。这个例子与音乐有关。斐波那契数列真是丰富多彩。 涉及音乐的节拍。设一个短音为一拍,用一字线 一 表示;一个长音时长为短音的两倍,为两拍,用二字线 一一 表示。用这两种声音奏出一小节的声音。那么具有n拍(n=1,2,3,)的一小节有几种不同的节奏类型?我们边举例子边说明什...
斐波那契点与斐波那契双曲线
浏览次今天所讲内容涉及很多知识内容,但都不难,也很有趣,不妨仔细读一读。 1 . 预备知识一:斐波那契数列的相关性质 性质A :三个相邻的斐波那契数,外侧两个斐波那契数的乘积,与中间斐波那契数的平方的差,绝对值为1;在中间数的项数为偶数时,外侧两数乘积比中间数的平方大1,在...
黄金分割比例是多少?诸葛亮黄金分割点是多少? 黄金分割比例分割点是 0.618, 什么是黄金分割? 生活中有哪些黄金分割的事物? 在生活中,有一个与众不同的数,按这个数所包含的比例关系组成 的事物通常表现出和谐与美。这个数就是 0.618, 即黄金数。为什么这个数如此有魅力呢?这...
斐波那契数列是怎么来的? 斐波那契数列与黄金数有什么联系? 意大利数学家斐波那契曾出过一道有趣的数学 题:如果一对兔子每月生一对小兔子,而每对小兔子在它们出生两个月后,又开始生一对小兔子。假定不发生意外的死亡,一对兔子一年后能繁殖多少对兔子?这个问题引出了一个...
阿拉伯数字是哪个国家发明的?阿拉伯数字是谁发明的?阿拉伯数字的由来 数字是表不数量的一种简便方法, Q在谁发明了数字的问题 上,大家说法不一 在我们生活中有很重要的位置。我们现在所使 用的数字是阿拉伯数字,它以十进制为基础,采用了十个计数符号: 0 、 1 、 2 、 3 、 4 、...
-ics,-logy,-graphy,-nomy,-ry都是学科的后缀(参考化学chemistry与牙科学dentistry的后缀是-ry?biology和biography差得有点远!经济Economy、生态学Ecology和经济学Economics看起来咋这么像?拓扑学Topology与地形学Topography咋这么相似呢?)。 另一个常见的学科后缀为-metry,如geometry(几何),stoichiometry(化学计量法...
斐波那契数列为: 1,1,2,3,5,8,13,21,34,55,89,144,233,377, 请问,斐波那契数列的第20项F20是否可以被3整除?是否可以被5整除?是否可以被11整除? 当然,我们可以按递推关系把F20找出来,那么,上述这三个整除是否可行就能够计算出来了。其实我们有更加快捷的方式说出上述三个问题的结果。这...
斐波那契数列数论性质与费马小定理
浏览次下面这个性质的出现次数非常多: 比如在那个著名的几何谬误中(以前讲过)。今天我们用这个性质来研究关于斐波那契数列中奇数项的因数的一个性质,这个性质一般不是很容易看出来。看出来了,证明也不是很容易。我今天应用费马小定理,就可以证明这个埋藏极深的性质。 数论性质...
卢卡斯数列与斐波那契数列
浏览次今天简单介绍一下卢卡斯数列。 我们知道斐波那契数列为: 1,1,2,3,5,8,13,21,34,55, 而卢卡斯数列是通过斐波那契数列来定义的。首先,我们补充定义F0=0。于是,补充后的斐波那契数列为: 0,1,1,2,3,5,8,13,21,34,55, 我们定义卢卡斯数为: Ln=Fn-1+Fn+1,其中n=1,2,3, 于是, L1=F0+F2=0+1=1 L2=F1+F3=1+2=3 L3=F2+F4=...
斐波那契数列的性质都有那些?
浏览次斐波那契数列的性质特别多。真是一个神奇的数列!今天就给您介绍这么几条。 第一组3条: 性质1 : 斐波那契数列前n项和等于第n+2项减1。用公式表示就是: 比如,前8项和: 1+1+2+3+5+8+13+21=55-1=54。 (第9项34没有出现。但其实它是最后两项的和。) 这条性质不难证明,如下: 相加,得...
斐波那契数列的大性质
浏览次今天讲斐波那契数列的一条很大的性质。说它大,是因为它涵盖了我们以前知道的多条性质。 这个大性质就是下面这个公式[其中的ui(下标i是正整数)都是斐波那契数]: 它说的是,斐波那契数列中任意两项的乘积与和它们等距离的另外两个斐波那契数的乘积之间的关系。下面我们就一一举例...
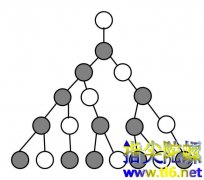
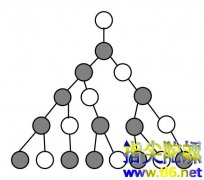
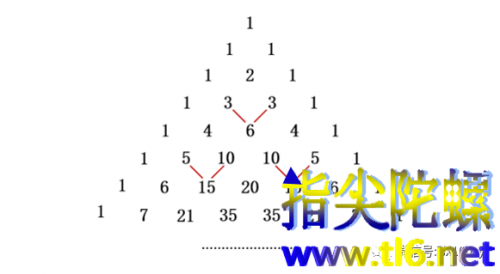
帕斯卡三角形和斐波那契数列
浏览次下图就是著名的帕斯卡三角形的前8行。它的一个重要性质就是:两腰上的数字全都是1,中间的数字,是它的肩上两个数字之和,即它的左上方数字和右上方数字之和。比如,6=3+3;15=5+10或15=10+5。 上图中您看出斐波那契数列在什么地方吗?似乎不太容易看出来吧。对,斐波那契数列没有直...