
今天我们研究斐波那契数列与集合的有趣的关系。我们首先定义由前n个正整数构成的集合Nn ={1,2,3,···,n}。那么在它的所有子集中,我们考虑没有任何两个元素是连续整数的那些子集。比如{1,3}是符合要求的,而{2,3}就不符合要求。我们认为一个元素构成的集合比如{1}或空集Φ都是符合要求的。我们的结论是,集合Nn这样的子集的个数等于斐波那契数列的第n+2项,即Fn+2。举例来说:
(1)n=1,集合N1={1},符合要求的子集有:
Φ,{1}
数量为2;而Fn+2=F3=2,正确。
(2)n=2,集合N2={1,2},符合要求的子集有:
Φ,{1},{2}
数量为3;而Fn+2=F4=3,也正确。
(3)n=3,集合N3={1,2,3},符合要求的子集有:
Φ,{1},{2},{3}
{1,3}
数量为5;而Fn+2=F5=5,仍然正确。
(4)n=4,集合N4={1,2,3,4},符合要求的子集有:
Φ,{1},{2},{3},{4}
{1,3},{1,4}
{2,4}
数量为8;而Fn+2=F6=8,正确。
(5)n=5,集合N5={1,2,3,4,5},符合要求的子集有:
Φ,{1},{2},{3},{4},{5}
{1,3},{1,4},{1,5}
{2,4},{2,5}
{3,5}
{1,3,5}
数量为13;而Fn+2=F7=13,仍然正确。
(6)n=6,集合N6={1,2,3,4,5,6},符合要求的子集有:
Φ,{1},{2},{3},{4},{5},{6}
{1,3},{1,4},{1,5},{1,6}
{2,4},{2,5},{2,6}
{3,5},{3,6}
{4,6}
{1,3,5},{1,3,6}
{1,4,6}
{2,4,6}
数量为21;而Fn+2=F8=21,仍然正确。
…………
您可以继续做下去,都将得出结论:集合Nn无相邻元素的子集的个数等于斐波那契数列的第n+2项,即Fn+2。但为什么呢?这样吧,我来给您一些提示。我也是突然发现的,发现的快乐无法形容。观察下图,我把这些子集涂以不同的颜色。观察不同颜色的子集。
Φ,{1},{2},{3},{4},{5},{6}
{1,3},{1,4},{1,5},{1,6}
{2,4},{2,5},{2,6}
{3,5},{3,6}
{4,6}
{1,3,5},{1,3,6}
{1,4,6}
{2,4,6}
您看出什么了吗?
●每个红色子集都有“6”作为其元素,且“6”是这些子集中最大的元素。称这些红色子集构成的集合为E6。红色子集的数量是8,即F6。也就是说,集合E6的大小为F6。
●依此类推,每个蓝色子集都有“5”作为它的元素,且“5”是这些子集中最大元素。称这些蓝色子集构成的集合为E5,蓝色子集的数量即E5的大小为F5=5。
●每个绿色子集都是其最大元素为“4”的集合,称这些绿色子集构成的集合为E4,绿色子集的数量即E4的大小为F4=3。
●每个粉色子集都是其最大元素为“3”的集合(注意,其他颜色的子集中也有可能有“3”,但那里的“3”不是最大的),称这些粉色子集构成的集合为E3,粉色子集的数量即E3的大小为F3=2。
●每个橙色子集都是其最大元素为“2”的集合,称这些橙色子集构成的集合为E2,橙色子集的数量即E2的大小为F2=1。
●每个青色子集都是其最大元素为“1”的集合,称这些青色子集构成的集合为E1,青色子集的数量即E1的大小为F1=1。
●最后,有一个由空集构成的集合:{Φ}。所以,上面这些由N6的全部无连续元素构成的子集构成的集合(姑且称其为A),就是E1,E2,E3,E4,E5,E6及{Φ}的并集:
A={Φ}∪E1∪E2∪E3∪E4∪E5∪E6
这个并集中全部子集的数量就是:
1+F1+F2+F3+F4+F5+F6
=1+1+1+2+3+5+8
=21
= F8
可以证明对任意正整数n,结论都是成立的。这个结论是斐波那契数列的一条性质,我们在第一章中讲到过(性质9)。即:
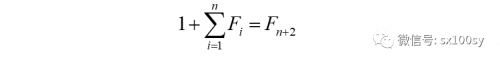
或
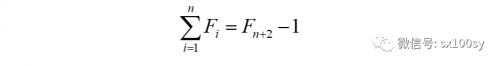
以上那些个子集都是一个个地“凑”出来的。其实,不用“凑”。可以从另一角度考虑问题。就比如,在前面写出N6的所有子集后,我们就可以在N6所有子集所形成的下面这个“表”的基础,写出以7为最大元素的一切子集E7。即在下面模式中,如何在红色子集的“右侧”增加出集合E7?
Φ,{1},{2},{3},{4},{5},{6}
{1,3},{1,4},{1,5},{1,6}
{2,4},{2,5},{2,6}
{3,5},{3,6}
{4,6}
{1,3,5},{1,3,6}
{1,4,6}
{2,4,6}
因为“6”与“7”相邻,所以,不可能在红色子集中增加“7”这个元素,而在非红色子集中则都可以增加“7”这个元素。于是,空集中加入“7”,就得到{7}。我们就把加入“7”后的子集写到上“表”红色子集的右侧。得到:
Φ,{1},{2},{3},{4},{5},{6};{7}
{1,3},{1,4},{1,5},{1,6};{1,7}
{2,4},{2,5},{2,6};{2,7}
{3,5},{3,6};{3,7}
{4,6};{4,7}
{5,7}
{1,3,5}, {1,3,6};{1,3,7}
{1,4,6}; {1,4,7}
{1,5,7}
{2,4,6};{2,4,7}
{2,5,7}
{3,5,7}
{1,3,5,7}
上“表”中,每行右侧加粗紫色为新增的所有“7”为其最大元素的子集。数量是13个,等于F7。上“表”中子集的总数为
1+F1+F2+F3+F4+F5+F6+F7
= 1+1+1+2+3+5+8+13
=34
= F9
我们今天把正整数集合的元素无连续整数的子集,与斐波那契数列联系了起来,用了一种形象的方法,很有趣。您慢慢体会一下。



















