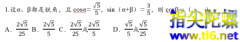缺8æ°
ææ³¢é£å¥æ°åä¸éå
æµè§æ¬¡å 为æç书ä¸æææ³¢é£å¥æ°åçé¦é¡¹å第2项ç¨F0åF1表示ï¼æ以为äºä¸å¼èµ·æ§ä¹ï¼è¿ééè¦é¦å éææ¬ç¯æç« ææ¶åçææ³¢é£å¥æ°åï¼å两项æ¯ç¨F1åF2表示çï¼å³F1=F2=1ãä¸é¢ï¼ä¸ºäºä½¿æ¨è¯»çæ¹ä¾¿ï¼å ååºææ³¢é£å¥æ°åçåä¸äºé¡¹ï¼ ä»å¤©æ们ç 究ææ³¢é£å¥æ°åä¸éåçæ趣çå ³ç³»ãæ们é¦å ...
é«ä¸é¶æ®µå¨ç 究å½æ°çè¿ç¨ä¸æ»æ¯ä¼ç¢°å°ååå¤æçå èåµå¥é®é¢,æ¯å¦ .è¿ç±»å½æ°ææ½è±¡å½æ°ä¹æå ·ä½å½æ°ï¼å¨åæå ¶é¶ç¹é®é¢çæ¶åï¼å¾å¤åå¦ä¼ç¸å½ç头ç¼ï¼æ¢ä¸è½ç»å¾ï¼ä¹ä¸è½ååºç¸åºç解æå¼é£å¯æä¹å¤æå? å ¶å®è¿ç±»å¾å¤æçå½æ°æä¸ä¸ªå¾ä¸ä¸çèç¹å½æ°é¶ç¹ï¼æ£æè°ç¬ç¹ä¹å¤å¿ ...
æ£æ´æ°å æ°ç个æ°å ¬å¼
æµè§æ¬¡ä¸ä¸ªæ£æ´æ°ï¼å¦æè½è¢«å¦ä¸ä¸ªæ£æ´æ°æ´é¤ï¼å°±è¯´è¿å¦ä¸ä¸ªæ´æ°æ¯è¿ä¸ªæ£æ´æ°çå æ°æé¤æ°ã æ¯å¦ï¼6å¯ä»¥è¢«1,2,3,6é½æ´é¤ï¼æ以ï¼1,2,3,6é½æ¯6çå æ°æé¤æ°ã ä¸ä¸ªæ£æ´æ°çå æ°ç个æ°æ¯ç¡®å®çï¼æ¯å¦6çå æ°ç个æ°æ¯4ï¼9çå æ°ç个æ°æ¯3ï¼1,3,9ï¼ã æ£æ´æ°å æ°ç个æ°ä¸è¿ä¸ªæ£æ´æ°ç大å°æ²¡æå ³...
æ¢ æ£®æ°ä¸æ¢ æ£®ç´ æ°ä¸å®å ¨æ°
æµè§æ¬¡ä»å¤©ç®åå°è®²ä¸è®²æ¢ 森æ°åæ¢ æ£®ç´ æ°ãä¸å¯è½æ¶åæ¢ æ£®æ°çæ¹æ¹é¢é¢ï¼èåªæ¯è®²ä¸è®²æ¯è¾å¥½ç解çæ¹é¢ãå½¢å¦ çæ°å«å æ¢ æ£®æ° ï¼å ¶ä¸pä¸ºç´ æ°ã å°±ç®æ¢ 森æ°çå®ä¹ä¸è¦æ±pæ¯ç´ æ°ï¼ä¹ä¸è½ä¿è¯æ¢ 森æ°ä¸å®æ¯ç´ æ°ãæ¢ æ£®æ°å¯è½æ¯ç´ æ°ï¼ä¹å¯è½ä¸æ¯ç´ æ°å³åæ°ãæ们ååºpååé¢ä¸äºç´ æ°æ¶çæ¢ ...
æ¢ æ£®æ°åæ¢ æ£®ç´ æ°
æµè§æ¬¡ä»å¤©ç®åå°è®²ä¸è®²æ¢ 森æ°åæ¢ æ£®ç´ æ°ãä¸å¯è½æ¶åæ¢ æ£®æ°çæ¹æ¹é¢é¢ï¼èåªæ¯è®²ä¸è®²æ¯è¾å¥½ç解çæ¹é¢ãå½¢å¦ çæ°å«å æ¢ æ£®æ° ï¼å ¶ä¸pä¸ºç´ æ°ã 为ä»ä¹è¿ä¸ªå®ä¹ä¸è¦æ±pæ¯ç´ æ°ï¼è¥pä¸åç´ æ°èååæ°ï¼é£ä¹ï¼2çåæ°æ¬¡æ¹ä¸å®æ¯ä¸ä¸ªå®å ¨å¹³æ¹æ°ï¼é£ä¹æ ¹æ®å¹³æ¹å·®å ¬å¼ï¼2çåæ°æ¬¡æ¹åå1ï¼å°±ä¸...
对äºå¤§å¤æ°é¢ç®æ¥è¯´ï¼ä¸å¤ªä¼åç¬ä½¿ç¨ä¹æ³åçåå æ³åçï¼é常é½æ¯ç»¼åè¿ç¨ã ä¸è¬çå½¢å¼ä¸ºï¼åä¸ä»¶äºæ ï¼æN个æ¥éª¤ï¼æ¯ä¸ªæ¥éª¤éååèªæä¸åçåç±»ï¼æ¯ä¸ªåç±»éåæå¤ç§æ¹æ³ï¼åæè æ¯ï¼åä¸ä»¶äºæ ï¼æN个åç±»ï¼æ¯ä¸ªåç±»éåæä¸åçæ¥éª¤ï¼æ¯ä¸ªæ¥éª¤éåæå¤ç§æ¹æ³ã æ»ä¹ï¼é...
æ们已ç»å¦è¿åå·®é®é¢æ¯å·²ç¥åä¸å·®ï¼ååé®é¢ä¹ç±»ä¼¼ï¼å°±æ¯å·²ç¥ä¸¤ä¸ªæ°çåä¸åæ°å ³ç³»ï¼æ±è¿2个æ°åå«æ¯å¤å°ãååé®é¢çåºæ¬å ¬å¼æ¯ï¼ ååé®é¢çåºæ¬å ¬å¼ 大æ°ï¼å°æ°ï¼ä¸¤æ°ä¹å 大æ°å°æ°ï¼åæ° å°æ°ï¼åï¼åæ°ï¼1ï¼ å¤§æ°ï¼åï¼å°æ° ååé®é¢å¦æä¸æ¯ç´æ¥ç»åºåæ°å ³ç³»ï¼èæ¯ç¨å¾®å...
æ°å½¢ç»åå¦ä¹ âé¤æ³è¿ç®å¾â
æµè§æ¬¡ä¸¥æ ¼æä¹ä¸æ¥è¯´ï¼é¤æ³æ²¡æè¿ç®å¾ãä½æ¯æ们å¯ä»¥æ ¹æ®æ°å½¢ç»åæè ä¹æ³è¿ç®å¾ï¼åç §çèªå·±ååºä¸ä¸ªè¿ç®å¾åºæ¥ã 1 é¤æ³äº¤æ¢å¾ï¼abcï¼acb æ们ççä¸å¾å¦ææ们æä¸ä¸ªå¤§é¿æ¹å½¢å 横åï¼å¹³ååæ4åï¼å°±ç¸å½äºå é¤ä»¥4ï¼ï¼ç¶ååç«åï¼ææ¯ä¸ªæ¨ªæ¡å¹³ååæ5åï¼å°±ç¸å½äºåé¤ä»¥5ï¼ï¼å¾å°...
ä»å¤©è®²ç±5æ¡å线ä½æ¤åãå¨å°å½±å ä½ä¸ï¼å¸æ¯å¡å®çä¸å¸éå®é¦å®çæ¯å¯¹å¶çãä»èå æ¥å 边形ä¸å¤åå 边形对å¶ãç¹ä¸çº¿å¯¹å¶ï¼å¯¹è¾¹ä¸å¯¹é¡¶ç¹å¯¹å¶ï¼å ±çº¿ä¸å ±ç¹å¯¹å¶ï¼ãæ以ä»å¤©çä½å¾å°±ä¸ä¸æç对å¶ã å ·ä½æ¥è¯´ï¼å ç»5æ¡å线ä¾æ¬¡åå1ï¼2ï¼3ï¼4ï¼5ãè¿éï¼å称æ¢å¯ä»¥è¡¨ç¤ºæ´æ¡å线ä¹å¯...
æ°å½¢ç»åå¦ä¹ ä¹æ³è¿ç®å¾
æµè§æ¬¡è¿ä¸èéè¿æ°å½¢ç»åå¦ä¹ ä¹æ³çä¸å¤§è¿ç®å¾ã 1 ä¹æ³äº¤æ¢å¾ï¼abï¼ba æ们å æ¥æ°ä¸æ°ï¼ä¸å¾ä¸æå 个å°æ¹åï¼ æ们ä¸è¡ä¸è¡çæ°ï¼æ¯ä¸è¡æ5个ï¼æ»å ±4è¡ï¼æ以æ¯ï¼ 5ï¼5ï¼5ï¼5ï¼54ï¼20 ä¹å¯ä»¥ä¸åä¸åçæ°ï¼æ¯ä¸åæ4个ï¼æ»å ±5è¡ï¼æ以æ¯ï¼ 4ï¼4ï¼4ï¼4ï¼4ï¼45ï¼20 æ 论æä¹æ°ï¼ 54ï¼45 æ们è½ç...
ä»å¤©æå°éèºç½å°ç¼åæ¥æ大家ä¸é è°±çå°æå·§äºã为ä»ä¹è¯´ä¸é è°±å¢ï¼å 为ä¸éç¨ï¼æ以ä¸é è°±ï¼æ¯ç«ææ¶åå¯è½æ为导æ°å¤§é¢çççæ¡æå¨ï¼ä¸è¿ä¹ææ¶åå¾é¸¡èï¼é£ä¹æ å³ã ä¸è¿æ³æ³å¨å导æ°çæ¶åååçè¿ä¸ªå¯ä»¥æçæ¡çåºæ¥ï¼é£çæ¡é½åºæ¥äºï¼è¿ç¨è¿å¾é¾åï¼ ç«¯ç¹æåº è¿å°±æ¯æ...
äºç¹å¯ä»¥å³å®ä¸ä¸ªæ¤åãé£ä¹ï¼å¨æ¤åä¸ä»»æéåäºä¸ªç¹ï¼ææ¤åæ¦æåï¼å¦ä½åæ ¹æ®è¿äºä¸ªç¹ä½åºè¿ä¸ªæ¤åå¢ï¼ åä¸ä¹ 讲è¿å¦ä½è¿æ¤åä¸ä¸ç¹ä½æ¤åçå线ï¼ãè¿æ¤åä¸ä¸ç¹ä½å线ãï¼é¾æ¥å¨æåï¼ï¼é£é使ç¨çæ¯å¸æ¯å¡å®çãä»å¤©çé®é¢ä¹æ¯å©ç¨å¸æ¯å¡å®çï¼æå ³å¸æ¯å¡å®ççå ·ä½å ...
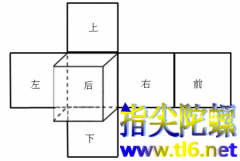
ç«ä½å¾çå¹³é¢å±å¼
æµè§æ¬¡ç«ä½å¾çå¹³é¢å±å¼åï¼ä¼æ¯ä»ä¹æ ·åå¢ï¼ 1 æ£æ¹ä½çå¹³é¢å±å¼ï¼ å®é ä¸ï¼æ£æ¹ä½çå¹³é¢å±å¼å¾è¿æå¾å¤ï¼å¯ä»¥è¯¦ç»ççãä¸ç½æå°½ç«æ¹ä½çå±å¼å¾ã 2 é¿æ¹ä½çå¹³é¢å±å¼ï¼ æ个ç¹ç¹ï¼å·¦å³ä¸¤åä¸æ ·å¤§ãä¸ä¸ä¸¤åä¸æ ·å¤§ãåå两åä¸æ ·å¤§ï¼ä½æ¯ä¸æ ·å¤§çé¨åé½ä¸ç¸é»ï¼ä¸ºä»ä¹ï¼èªå·±æ³ä¸æ³ï¼...
æ¤åçå ±è½ç´å¾çå¾è§£
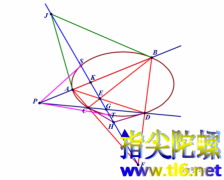
æµè§æ¬¡ä¸ä¸¤è®²æ们讲è¿ä»æ¤åå¤ä¸ç¹ä½æ¤åå线ï¼è¿è®²äºææ¤åå¤è¿ä¸ªç¹ä½ä¸ºæç¹æ¶ï¼æç¹çæ线æ¯ä»ä¹ãæç¹å°æ¤å两æ¡å线çåç¹çè¿çº¿å°±æ¯è¿æ¡æ线ãæ¯å¦ä¸å¾ä¸ç¹Pè¥ä¸ºæç¹ï¼åå®çæ线就æ¯è¿åç¹SåTçç´çº¿ã 请é®ï¼æ线ä»ä¹æ¶åéè¿æ¤åä¸å¿ï¼ å¯ä»¥çåºï¼è¥ç¹P离æ¤åè¶æ¥è¶è¿ï¼å两æ¡...
ä»å¤©éè¿ä¸¤ä¸ªèåçå®çå¸æ¯å¡å®çåå¸éå®é¦å®çæ¥è®²ä¸è®²å°å½±å ä½çå å¨ç¾ï¼æå¸æ¯å¡å®çåå¨å°±ä¸å®æå¸éå®é¦å®çåå¨ï¼åä¹äº¦ç¶ã两个å®çæ¯é æ对å¶çã以æ¤å为ä¾ï¼å¯¹åé¥æ²çº¿é½æ£ç¡®ã ABCDEF为æ¤åçå æ¥å 边形ãa,b,c,d,e,fåå«ä¸ºæ¤åå¨ç¹A,B,C,D,E,Få¤çå线ãå æ¡å线å´æä¸ä¸ª...
ä»å¤©è®²ä¸ä¸ªä»æ¤åå¤ä¸ç¹ä½æ¤åå线çç»å¦æ¹æ³ æ们åªç¥éä¸ä¸ªç¥¼æ¤ååæ¤åå¤ä¸ç¹P å¦ä¸å¾æ示 æè¿éæè°è£¸æ¤åæ¯ææ¤åæ¬èº«ï¼èå®çä¸å¿ãç¦ç¹ã顶ç¹ãå线ä¸æ¦ä¸ç¥ æ以éåç¨å°å½±å ä½å¦çæ¹æ³ å°å½±å ä½å¦çæ¹æ³é常ç®åï¼ä½æ¹æ³èåçç论就ä¼æ¯è¾æ·±å¥¥ æå æ¥è®²ä¸è®²ä½æ³ ï¼...
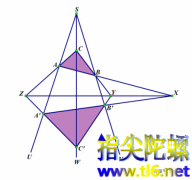
å°±ææç¥ï¼æ好å 个å®çé½ç§°ä½å¸éå®é¦å®çï¼ä»å¤©ææ¥è¯´ä¸è¯´å ¶ä¸ä¸ç§ã å¸éå®é¦å®ç ï¼å¦æä¸ä¸ªå 边形ä¸ç»äºç¸é´éçä¸æ¡è¾¹äº¤äºä¸ç¹ï¼å¦ä¸ç»äºç¸é´éçä¸æ¡è¾¹ç¸äº¤äºå¦ä¸ç¹ï¼é£ä¹è¿ä¸ªå 边形ä¸æ¡ç¸å¯¹é¡¶ç¹è¿çº¿ï¼å¯¹è§çº¿ï¼ç¸äº¤äºä¸ç¹ã å®çåªç¨è¯è¨æè¿°ï¼ä¸å¤ªå¥½ç解ãæ们ç»å¾ä¸¾ä¾...
对æ°å¹³åä¸çå¼çå®ä¹ä¸è¯æ
æµè§æ¬¡å ³äºä¸¤ä¸ªæ£æ°çç®æ¯å¹³åå¼åå ä½å¹³åå¼ï¼æ们å¨å¦ä¹ åå¼ä¸çå¼çæ¶å就已ç»é常çç»äºï¼åæ¶æç¸ä¿¡å¨è®²åå¼ä¸çå¼çæ¶åï¼å¤§å®¶çèå¸ä¸å®ä¹æå±è¿ ä¸å¹³æ¹å¹³åæ° ãåæ¶æ们ä¹ç¥é é£ä¹è½ç¶æ们ç¥éäºè¿åç§ä¸ççåå¼æ满足çå ³ç³»ï¼ä½æ¯å¯¹äºæ们æçæçå ä½å¹³åå¼åç®æ¯å¹³åå¼...
æä¸ä¸ªé®é¢ï¼ä¸ç¥æ¯è°æåºæ¥çãè¿ä¸ªé®é¢æ¯ï¼è¦æå棵æ æ ½ç§æåè¡ï¼æ¯è¡é½æä¸æ£µæ ãé®åºè¯¥æä¹æ ½ç§ï¼ ï¼0ï¼å¨2016å¹´1æ5æ¥è®²è¿ä¸ä¸ªç±»ä¼¼çé®é¢ï¼å³è¦æ±ç§ä¹æ£µæ ï¼è¿ä¹æ£µæ å¯ä»¥è¿æ¥åºåæ¡çº¿ï¼æ¯æ¡çº¿ä¸é½æä¸å¤ä¸å°ä¸æ£µæ ãå¨é£éï¼ææ¯åæ¤é®é¢å¼åºå¸æ®æ¯å®ççãå ·ä½å 容详è§æ...
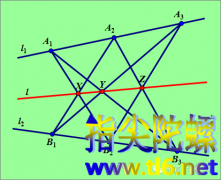
å¸æ®æ¯å®ç å°è© 家åé¢æä¸ç空å°ï¼å¥¹æ³å¨ä¸é¢ç§æ¤ä¹æ£µè¹ææ ï¼ä½è¦æ±è½å¤è¿æ¥åºåæ¡çº¿æ®µï¼èæ¯æ¡çº¿æ®µé½è¿ä¸æ£µæ ãé®å¥¹éè¦æä¹ç§æ¤è¿ä¹æ£µæ ï¼ æ¬æè¦ä»ç»çå¸æ®æ¯å®çå¯ä»¥ç¨æ¥è§£å³è¿ä¸ªé®é¢ã ä¸æ¡ç´çº¿ä¸æ顺åºä¸ç¹A1ãA2ãA3ï¼å¦ä¸æ¡ç´çº¿ä¸æä¸A1ãA2ãA3顺åºä¸è´çä¸ç¹B1ãB2ãB...
æ·±å¤ï¼å¨ç¢ç£¨ä¹åéå°çä¸ä¸ªä¸è§å½æ°çèå´å¤å®é®é¢ ææ¶åè½ç¶ååºæ¥äºï¼ä½æ¯æ¯ä¸ªé¢æ¹æ³ä¸ä¸æ ·ï¼æå°±ä¼æ³ï¼ 为ä»ä¹è¿ä¸ªé¢ï¼æè¿æ ·åï¼é£ä¸ªé¢æé£æ ·åï¼ä¸ºä»ä¹æä¼è¿æ ·æ³ï¼ä¸ºä»ä¹é£æ ·åºä¸æ¥ï¼ åªææ³æ¸ æ¥è¿ä»¶äºï¼ä¸æ¥ï¼èªå·±ä¸ä¼å¿ï¼äºæ¥ï¼æè½ç»å¦çæè¿ä¸ªé®é¢è®²æç½ï¼å¦å说å...
没æ顶ç¹ï¼å¯¹è§çº¿æä¹ç»ï¼
æµè§æ¬¡è¿ä¸ªé¢ç®æ¯è¿æ ·çï¼æä¸ä¸ªå边形ABCDï¼ç»å¨ä¸å¼ ç½çº¸ä¸ãæ¬æ¥å°±æ¯æ³ç®åå°ç»åºä¸¤æ¡å¯¹è§çº¿ç交ç¹Sãå¦ä¸å¾æ示ã ä½æ¯ä¸ç¥ä»ä¹åå ï¼ç»æå边形ABCDç纸ä¸ï¼ç¹Båç¹Dåå ¶å¤ä¾§è¢«ææäºï¼æ为ä¸å¾æ示çæ ·åã äºæ¯ï¼è½ç¶å¯¹è§çº¿ACä»ç¶å¯ä»¥ç»åºï¼ä½æ²¡æäºç¹BåDï¼å°±æ æ³ç»åºå¯¹è§çº¿BDï¼ä»...
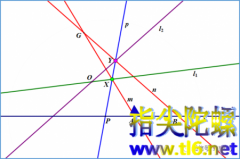
ç¬æ²æ ¼å®çè¯æ:轨迹æ¯ç´çº¿
æµè§æ¬¡ä»å¤©è®²ä¸ä¸ªè½¨è¿¹é¢ï¼æ们å°ç¨ç¬æ²æ ¼å®çè¯æè¿ä¸ªè½¨è¿¹æ¯ä¸æ¡ç´çº¿ã é¢ç®æ¯è¿æ ·çï¼æ两æ¡ç¸äº¤ç´çº¿l1(绿è²)ål2(ç´«è²)ï¼äº¤ç¹ä¸ºOãå¦æä¸æ¡ç´çº¿l(æ·±èè²)ï¼å ¶ä¸æä¸ä¸ªå®ç¹PãAåBãè¿ç¹Pä½ç´çº¿p(天èè²)ï¼ä¸ç´çº¿l1ål2åå«äº¤äºä¸¤ç¹X(绿ç¹)åY(ç²ç¹)ãå¦ä¸å¾æ示ãè¿ç´çº¿lä¸çç¹Aåç´çº¿l1ä¸ç...
éä½ç¸åæ³æä¹åï¼
æµè§æ¬¡éä½ç¸åæ³å¯è½æ¯é«ä¸å¦ççå©æ¢¦ï¼ææç¥éæä¹ç®ï¼ä½æ¯æ»æ¯ç®ä¸åºæ£ç¡®çæ¡ãçå°çæ åçæ¡åèªå·±ççæ¡å®å ¨ä¸ä¸æ ·ï¼ä½æ¯æ¹æ³å®å ¨æ£ç¡®ï¼å¯æ¯èªå·±å°±æ¯ä¸è½ç®åºçæ£ççæ¡ã â è¿å¾å¤§ç¨åº¦ä¸å¯è½æ们å¨è®¡ç®æ°åéä½ç¸åçæ¶ååªæ¯æ³¨éç®åç计ç®ï¼è没æçå°éä½ç¸åçæ¬è´¨ã...
æ诡å¼æ°å¦æ论ï¼1+1=1ãè¶ çº§é¦æ°åå ¸ãåçæ论ãå¸å°ä¼¯ç¹æ é¦æ论...
æµè§æ¬¡æ论 å²ä¸æ诡å¼çæ论 ä»å¤©ï¼8å²è¡¨å¦¹çèå¸ç»å¥¹å¥å±äºä¸å大巧å åï¼éèºç½å°ç¼æ趣她è½ä¸è½åç»æç¹ï¼éå°æ®å¿æç»ï¼éèºç½å°ç¼å¾æ¤æï¼æä¸å³å¿è¦ç¥ä¸ç¥é¬¼ä¸è§å°åä¸è¡¨å¦¹çå·§å åã éèºç½å°ç¼è¶è¡¨å¦¹å¨è®¤çåä½ä¸çæ¶åï¼çµæºä¸éªï¼æ¿èµ·åå°±æ¯åï¼å·å·åäºå¥½å åã åè£ å¸®è¡¨...
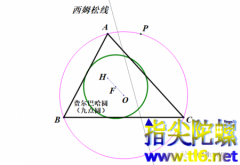
ä»å¤©è®²ä¸ä¸ªæ¼äº®çå¾å½¢ï¼è¯·å çä¸çå®çå¨ç»ã ï¼1ï¼ è¥¿å§æ¾çº¿ ä»ä¸è§å½¢å¤æ¥åä¸ä¸ç¹Påä¸è§å½¢ä¸æ¡è¾¹å¼å线ï¼ä¸ä¸ªå足ä¸å®ä½äºä¸æ¡ç´çº¿ä¸ãè¿æ¡ç´çº¿å°±å«å西å§æ¾çº¿ã éçç¹På¨å¤æ¥åä¸è¿å¨ä¸å¨ï¼è¥¿å§æ¾çº¿æåæ¹åæ转åå¨ï¼å¯å次è§çä¸é¢çå¨ç»ï¼ã西å§æ¾çº¿çå ç»æ¯ä¸ä¸ªå°ç¹ä¸...
å¦ä¹ äºé¤æ³ç表妹è·æ¥é®æï¼ ä¸ºä»ä¹ä¸è½é¤ä»¥0ï¼ å°±è¿ä¸ªé®é¢ï¼æä¸é¨è¯·æ¥äºé«å·ç Siri ã åæ ·æ¯æ°åï¼0为ä»ä¹å°±ä¼è¿ä¹æ¨å¢ï¼ å°å¦ç å°å¦èå¸ä¼ç´æ¥ç»ä½ æ¥ä¸å¥ï¼ å«é®ï¼é®å°±æ¯æ²¡æä¹ï¼ æä¹ç解ï¼æ们说12å¯ä»¥ç解为1个ä¸è¥¿åæ2份ã åæ ·ï¼13å¯ä»¥ç解为1个ä¸è¥¿åæ3份ã ä½æ¯ï¼10å¯ä»¥...
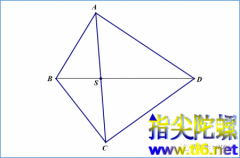
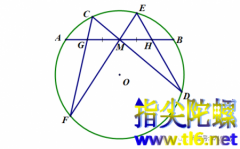
æ¢ æ¶ å³æ¯å®çè¯æè´è¶å®ç
æµè§æ¬¡è´è¶å®çï¼ AB为åOçä»»æä¸æ¡å¼¦ï¼M为ABçä¸ç¹ï¼CDåEF为è¿ç¹Mç两æ¡ä¸åäºABç弦ãè¿æ¥CFï¼DEï¼è¿ä¸¤æ¡å¼¦ä¸AB交äºç¹GåHãé£ä¹ï¼GM=MHã è¯æ ï¼å¦ä¸å¾æ示ã è¯æ ï¼å°±ä¸å¾çæ ·åï¼æ们延é¿FCåDEï¼ä¸¤å»¶é¿çº¿ç¸äº¤äºç¹Pã äºæ¯å¾å°ä¸è§å½¢GPHãèCMDåEMFé½æ¯ä¸ä¸è§å½¢GPHä¸è¾¹ï¼æ延é¿çº¿ï¼é½ç¸äº¤...
âå®åå¹åâä¸ä¸è§å½¢ä½å¾
æµè§æ¬¡ä»å¤©ç»åºä¸ä¸ªéè¦ç»è®ºï¼ç¶åå©ç¨è¿ä¸ªç»è®ºè§£ä¸éä¸è§å½¢ä½å¾é¢ãå ¶ä¸ç¨å°ä¹åä¸è¿çææ讲è¿ç代æ°è§£ææ³ã æ们ç¥éï¼å¦æä¸å¨ç¹å°ä¸æ¡å®çº¿æ®µä¸¤ä¸ªç«¯ç¹çè·ç¦»çå¹³æ¹åçäºè¿æ¡å®çº¿æ®µé¿åº¦çå¹³æ¹ï¼é£ä¹è¿æ ·çå¨ç¹è¿å¨ç轨迹ææ¾æ¯ä¸ä¸ªåï¼æ ¹æ®å¾è¡å®ççéå®çï¼ã ä»ç¶æ¯è¿ä¸çº¿æ®µ...
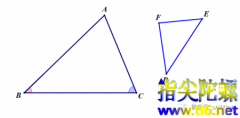
å¦å¾ï¼æä¸ä¸ªç¨å¤§ä¸äºçä¸è§å½¢ABCï¼è¦æ±å¨å ¶å é¨ä½ä¸ä¸ªä¸è§å½¢ï¼ä¸ä¸ªé¡¶ç¹åå«ä½äºç¨å¤§ä¸è§å½¢çä¸æ¡è¾¹ä¸ï¼è¿æ ·ä½åºçä¸è§å½¢ç§°ä¸ºå æ¥ä¸è§å½¢ï¼ï¼ä½¿å ¶ä¸æå·²ç¥è¾å°ä¸è§å½¢DEFå ¨çã 请èèä¸ä¸ãæ¯ä¸æ¯æ²¡ææè·¯ï¼é£ä¹æ们ä¸å¦¨éåæç»´ï¼å³è½å¦ä»ç¨å°ä¸è§å½¢DEFåºåï¼ä½åºä¸ä¸ªä¸ä¸è§å½¢A...